
科目: 来源: 题型:
【题目】已知椭圆![]() 的两焦点在
的两焦点在![]() 轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为
轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆的方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以线段
,使得以线段![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() .
. ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 上任意一点.
上任意一点.
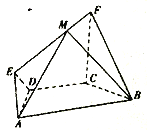
(1)求证: ![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动(包括两端点),若平面
上运动(包括两端点),若平面![]() 与平面
与平面![]() 所成的锐二面角为60°,试确定点
所成的锐二面角为60°,试确定点![]() 的位置.
的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月(5-10)月)的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示.
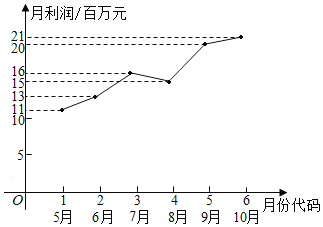
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并据此预测该公司2020年5月份的利润;
的线性回归方程,并据此预测该公司2020年5月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料损坏的年限不同,现对
两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料损坏的年限不同,现对![]() 两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计表(表).若从产品使用寿命的角度考虑,甲公司的负责人选择采购哪款新型材料更好?
两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计表(表).若从产品使用寿命的角度考虑,甲公司的负责人选择采购哪款新型材料更好?
使用寿命 | 1个月 | 2个月 | 3个月 | 4个月 | 总计 |
材料类型 | |||||
| 20 | 35 | 35 | 10 | 100 |
| 10 | 30 | 40 | 20 | 100 |
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() ,其中
,其中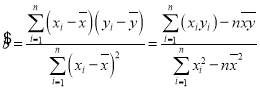 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点.点
两点.点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() .
.

(1)求抛物线线![]() 的标准方程;
的标准方程;
(2)问直线![]() 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校设计了一个实验考察方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中2道题的便可通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成,考生乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲、乙两考生正确完成题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,O为坐标原点,以O为圆心的圆与直线
中,O为坐标原点,以O为圆心的圆与直线![]() 相切.
相切.
(1)求圆O的方程.
(2)直线![]() 与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形
与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形![]() 为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由.
为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
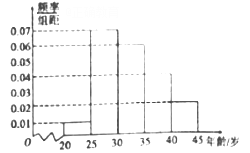
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com