
科目: 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第1组
人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
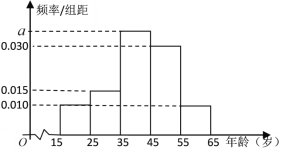
(1)求![]() 的值;
的值;
(2)求出样本的平均数(同一组数据用该区间的中点值作代表);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行问卷调查,求第2组中抽到
人进行问卷调查,求第2组中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】进入12月以业,在华北地区连续出现两次重污染天气的严峻形势下,我省坚持保民生,保蓝天,各地严格落实机动车限行等一系列“管控令”,某市交通管理部门为了了解市民对“单双号限行”的态度,随机采访了200名市民,将他们的意见和是否拥有私家车的情况进行了统计,得到如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断能否在犯错误的概率不超过![]() 的前提下认为“对限行的态度与是否拥有私家车有关”;
的前提下认为“对限行的态度与是否拥有私家车有关”;
(2)为了了解限行之后是否对交通拥堵、环境染污起到改善作用,从上述调查的不赞同限行的人员中按是否拥有私家车分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人没有私家车的概率.
附: 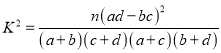 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:

(1)根据表中的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面直角坐标系上一动点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的2倍。
的距离的2倍。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 与点
与点![]() 关于点
关于点![]() 对称,求
对称,求![]() ,
,![]() 两点间距离的最大值。
两点间距离的最大值。
(3)若过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() ,则是否存在直线
,则是否存在直线![]() ,使
,使![]() 取得最大值,若存在,求出此时
取得最大值,若存在,求出此时![]() 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】单位圆的内接正n(n≥3)边形的面积记为![]() ,则f(3)=_____; 下面是关于
,则f(3)=_____; 下面是关于![]() 的描述:
的描述:
③![]()
![]() ④
④![]()
![]()
![]()
其中正确结论的序号为__________.(注:请写出所有正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下面类比推理:
①“若2a<2b,则a<b”类比推出“若a2<b2,则a<b”;
②“(a+b)c=ac+bc(c≠0)”类比推出“![]() (c≠0)”;
(c≠0)”;
③“a,b∈R,若a-b=0,则a=b”类比推出“a,b∈C,若a-b=0,则a=b”;
④“a,b∈R,若a-b>0,则a>b”类比推出“a,b∈C,若a-b>0,则a>b(C为复数集)”.
其中结论正确的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合空间向量数量积的运算法则计算可得![]() ,
,![]() .则
.则![]() ,
,![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐标计算可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
试题解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【题型】解答题
【结束】
19
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 上任意一点到两焦点
上任意一点到两焦点![]() 距离之和为
距离之和为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.点
两点.点![]() 为椭圆上一点,求
为椭圆上一点,求![]() 的面积的最大值及此时直线
的面积的最大值及此时直线![]() 的直线方程.
的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com