
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线![]() 的准线与
的准线与![]() 轴的交点为
轴的交点为![]() ,过
,过![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() 两点.
两点.
(1)求线段![]() 中点的轨迹;
中点的轨迹;
(2)若线段![]() 的垂直平分线交对称轴于
的垂直平分线交对称轴于![]() ),求
),求![]() 的取值范围;
的取值范围;
(3)若直线的斜率依次取![]() 时,线段
时,线段![]() 的垂直平分线与对称轴的交点依次为
的垂直平分线与对称轴的交点依次为
![]() ,当
,当![]() 时,
时,
求:![]()
![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】目前,某市出租车的计价标准是:路程2![]() 以内(含2
以内(含2![]() )按起步价8元收取,超过2
)按起步价8元收取,超过2![]() 后的路程按1.9元/km收取,但超过15
后的路程按1.9元/km收取,但超过15![]() 后的路程需加收50%的返空费(即单价为
后的路程需加收50%的返空费(即单价为![]()
![]() 元/
元/![]() ).
).
(1)若![]() ,将乘客搭乘-次出租车的费用
,将乘客搭乘-次出租车的费用![]() (单价:元)表示为行程
(单价:元)表示为行程![]() (单位:
(单位:![]() )的分段函数;
)的分段函数;
(2)某乘客行程为16![]() ,他准备先乘一辆出租车行驶8
,他准备先乘一辆出租车行驶8![]() ,然后再换乘另一辆出租车完成余下路程,请问:他这样做是否比只乘一辆出租车完成全程更省钱?
,然后再换乘另一辆出租车完成余下路程,请问:他这样做是否比只乘一辆出租车完成全程更省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
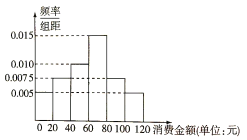
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:

![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列结论中正确的是( )
A.已知函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 在任何区间内的平均变化率均比
在任何区间内的平均变化率均比![]() 在同一区间内的平均变化率小,则函数
在同一区间内的平均变化率小,则函数![]() 在
在![]() 上是减函数;
上是减函数;
B.已知总体的各个个体的值由小到大依次为2,3,3,7,10,11,12,![]() ,18,20,且总体的平均数为10,则这组数的75%分位数为13;
,18,20,且总体的平均数为10,则这组数的75%分位数为13;
C.方程![]() 的解集为
的解集为![]() ;
;
D.一次函数![]() 一定存在反函数.
一定存在反函数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的图象中相邻两条对称轴之间的距离为
的图象中相邻两条对称轴之间的距离为![]() ,且直线
,且直线![]() 是其图象的一条对称轴.
是其图象的一条对称轴.

(1)求![]() ,
,![]() 的值;
的值;
(2)在图中画出函数![]() 在区间
在区间![]() 上的图象;
上的图象;
(3)将函数![]() 的图象上各点的横坐标缩短为原来的
的图象上各点的横坐标缩短为原来的![]() (纵坐标不变),再把得到的图象向左平移
(纵坐标不变),再把得到的图象向左平移![]() 个单位,得到
个单位,得到![]() 的图象,求
的图象,求![]() 单调减区间.
单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com