
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.

问:(1)这个几何体是什么?
(2)这个几何体由几个面构成?每个面的三角形是什么三角形?
查看答案和解析>>
科目: 来源: 题型:
【题目】下列结论中正确的个数是( )
①正三棱锥的顶点在底面的射影到底面各顶点的距离相等;
②有两个侧面是矩形的棱柱是直棱柱;
③两个底画平行且相似的多面体是棱台;
④底面是正三角形,其余各面都是等腰三角形的三棱锥一定是正三棱锥.
A.0B.1C.5D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P.
(Ⅰ)求过点P且平行于直线3x+4y﹣15=0的直线![]() 的方程;(结果写成直线方程的一般式)
的方程;(结果写成直线方程的一般式)
(Ⅱ)求过点P并且在两坐标轴上截距相等的直线![]() 方程(结果写成直线方程的一般式)
方程(结果写成直线方程的一般式)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=![]() ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB=![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.

查看答案和解析>>
科目: 来源: 题型:
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值
为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品,当
时,产品为二级品,当![]() 时,产品为三级品,现用两种新配方(分别称为
时,产品为三级品,现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了100件这种产品,
配方)做实验,各生产了100件这种产品,
并测量了每件产品的质量指标值,得到下面的试验结果:(以下均视频率为概率)
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
|
频数 | 5 | 10 | 15 | 40 | 30 |
(Ⅰ)若从![]() 配方产品中有放回地随机抽取3件,记“抽出的
配方产品中有放回地随机抽取3件,记“抽出的![]() 配方产品中至少1件二级品”为事件
配方产品中至少1件二级品”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;
;
(Ⅱ)若两种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下关系:
满足如下关系: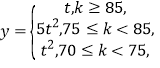 其中
其中![]() ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长轴为直径的圆与直线
的长轴为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知过点![]() 的动直线与椭圆
的动直线与椭圆![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的面积S的取值范围.
的面积S的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)![]() 是R上的奇函数.
是R上的奇函数.
(1)若x∈[![]() ,
,![]() ],求f(x)的取值范围
],求f(x)的取值范围
(2)若对任意的x1∈[1,![]() ,总存在x2∈[
,总存在x2∈[![]() ,
,![]() ]使得mlog2(﹣6x12+24x1﹣16)﹣f(x2)
]使得mlog2(﹣6x12+24x1﹣16)﹣f(x2)![]() 0(m>0)成立,求实数m的取值范围.
0(m>0)成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,![]() φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0
φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0![]() ,﹣2),
,﹣2),
(1)若函数f(x)的最小正周期为π,求函数f(x)的解析式;
(2)当x∈(x0,x0![]() )时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[
)时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[![]() ,
,![]() ]上有且仅有一解,求实数a的取值范围.
]上有且仅有一解,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的焦点分别为
)的焦点分别为![]() ,
,![]() ,离心率
,离心率![]() ,过左焦点的直线与椭圆交于
,过左焦点的直线与椭圆交于![]() ,
,![]() 两点,
两点,![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆有两个不同的交点
与椭圆有两个不同的交点![]() ,
,![]() ,且点
,且点![]() 在点
在点![]() ,
,![]() 之间,试求
之间,试求![]() 和
和![]() 面积之比的取值范围(其中
面积之比的取值范围(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com