
科目: 来源: 题型:
【题目】已知函数![]() 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为![]()
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴正方向向右平移
轴正方向向右平移![]() 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,当
的图象,当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数的上界.已知函数
称为函数的上界.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知奇函数f(x)=a-![]() (a∈R,e为自然对数的底数).
(a∈R,e为自然对数的底数).
(1)判定并证明f(x)的单调性;
(2)若对任意实数x,f(x)>m2-4m+2恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线C1:![]() ,曲线C2:
,曲线C2: .
.
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线![]() ,
,![]() .写出
.写出![]() ,
,![]() 的参数方程.
的参数方程.![]() 与
与![]() 公共点的个数和C1与C2公共点的个数是否相同?说明你的理由.
公共点的个数和C1与C2公共点的个数是否相同?说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】曲一中某研究性学习小组对学习数学的练习时间与进步率的关系进行研究,他们分别记录了同班5个同学一周内的学习时间与周测成绩进步率,得到如下资料.

(1)从5个同学中任选2个,记其进步率分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)若进步率![]() 与学习时间
与学习时间![]() 服从线性关系,求出
服从线性关系,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)在这5个同学中任取3个,其中进步率超过25的有![]() 个同学,求
个同学,求![]() 的数学期望.
的数学期望.
参考公式:回归直线方程是![]() ,其中
,其中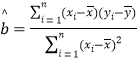
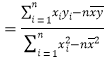
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的最值.
的距离的最值.
【答案】(1)![]() ,
, ![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为![]()
【解析】试题分析:(1)根据参数方程和极坐标化普通方程化法即易得结论![]() 的普通方程为
的普通方程为![]() ;直线
;直线![]() 的普通方程为
的普通方程为![]() .(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设
.(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设![]() ,
, ![]()
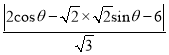
![]()
 .即可得出最值
.即可得出最值
解析:(1)根据题意,由 ,得
,得![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 的普通方程为
的普通方程为![]() ;
;
由![]() 及
及![]() ,
, ![]() 得
得![]() ,
,
故直线![]() 的普通方程为
的普通方程为![]() .
.
(2)由于![]() 为曲线
为曲线![]() 上任意一点,设
上任意一点,设![]() ,
,
由点到直线的距离公式得,点![]() 到直线
到直线![]() 的距离为
的距离为
![]()

![]()
 .
.
∵![]()
![]() ,
,
∴
 ,即
,即![]()
![]() ,
,
故点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() ,最小值为
,最小值为![]() .
.
点睛:首先要熟悉参数方程和极坐标方程化普通方程的方法,第一问基本属于送分题所以务必抓住,对于第二问可以总结为一类题型,借助参数方程设点的方便转化为三角函数最值问题求解
【题型】解答题
【结束】
23
【题目】已知函数![]() ,
,![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)若函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的上方,求
图象的上方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为![]() ,
,![]() ,
,![]() ,
,![]() 的中点,在此几何体中,给出下面五个结论:①平面
的中点,在此几何体中,给出下面五个结论:①平面![]() 平面ABCD;②
平面ABCD;②![]() 平面BDG;③
平面BDG;③![]() 平面PBC;④
平面PBC;④![]() 平面BDG;⑤
平面BDG;⑤![]() 平面BDG.
平面BDG.
其中正确结论的序号是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com