
科目: 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是
旋转过程中的一个图形,下列命题中,错误的是

A. 恒有![]() ⊥
⊥![]()
B. 异面直线![]() 与
与![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解中学生课余观看热门综艺节目“爸爸去哪儿”是否与性别有关,某中学一研究性学习小组从该校学生中随机抽取了![]() 人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的
人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的![]() ,男生喜欢看该节目的占男生总人数的
,男生喜欢看该节目的占男生总人数的![]() .随后,该小组采用分层抽样的方法从这
.随后,该小组采用分层抽样的方法从这![]() 份问卷中继续抽取了
份问卷中继续抽取了![]() 份进行重点分析,知道其中喜欢看该节目的有
份进行重点分析,知道其中喜欢看该节目的有![]() 人.
人.
(1) 现从重点分析的![]() 人中随机抽取了
人中随机抽取了![]() 人进行现场调查,求这两人都喜欢看该节目的概率;
人进行现场调查,求这两人都喜欢看该节目的概率;
(2) 若有![]() 的把握认为“爱看该节目与性别有关”,则参与调查的总人数
的把握认为“爱看该节目与性别有关”,则参与调查的总人数![]() 至少为多少?
至少为多少?
参考数据:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂有120名工人,其年龄都在20~ 60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分成四组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备。现采用分层抽样法从全厂工人中抽取一个容量为20的样本参加新设备培训,培训结束后进行结业考试。已知各年龄段培训结业考试成绩优秀的人数如下表所示:

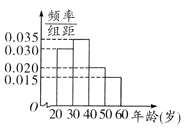
若随机从年龄段[20,30)和[40,50)的参加培训工人中各抽取1人,则这两人培训结业考试成绩恰有一人优秀的概率为___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线 y = x3 + x-2 在点 P0 处的切线![]() 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线![]() , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
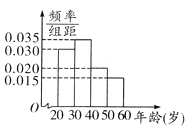
【题目】某工厂有120名工人,其年龄都在20~ 60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分成四组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试。已知各年龄段两项培训结业考试成绩优秀的人数如下表所示。假设两项培训是相互独立的,结业考试也互不影响。
年龄分组 | A项培训成绩 优秀人数 | B项培训成绩 优秀人数 |
[20,30) | 27 | 16 |
[30,40) | 28 | 18 |
[40,50) | 16 | 9 |
[50,60] | 6 | 4 |
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求四个年龄段应分别抽取的人数;
(2)根据频率分布直方图,估计全厂工人的平均年龄;
(3)随机从年龄段[20,30)和[40,50)中各抽取1人,设这两人中A、B两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com