
科目: 来源: 题型:
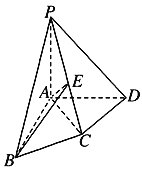
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
查看答案和解析>>
科目: 来源: 题型:
【题目】常州地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔 ![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() .经测算,地铁载客量与发车时间间隔
.经测算,地铁载客量与发车时间间隔![]() 相关,当
相关,当![]() 时地铁为满载状态,载客量为1200人,当
时地铁为满载状态,载客量为1200人,当![]() 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与![]() 的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为
的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为![]() .
.
⑴ 求![]() 的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
⑵ 若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】中国是世界互联网服务应用最好的国家,一部智能手机就可以跑遍国内所有地方,中国市场的移动支付普及率高得惊人.一家大型超市委托某高中数学兴趣小组调查该超市的顾客使用移动支付的情况,调查人员从年龄在![]() 内的顾客中,随机抽取了
内的顾客中,随机抽取了![]() 人,调查他们是否使用移动支付,结果如下表:
人,调查他们是否使用移动支付,结果如下表:
年龄 |
|
|
|
|
|
|
|
|
使用 |
|
|
|
|
|
|
|
|
不使用 |
|
|
|
|
|
|
|
|
(1)为更进一步推动移动支付,超市准备对使用移动支付的每位顾客赠送![]() 个环保购物袋,若某日该超市预计有
个环保购物袋,若某日该超市预计有![]() 人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为使用移动支付与年龄有关?
的把握认为使用移动支付与年龄有关?
年龄 | 年龄 | 小计 | |
使用移动支付 | |||
不使用移动支付 | |||
合计 |
附:下面的临界值表供参考:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
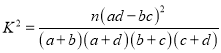 ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
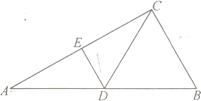
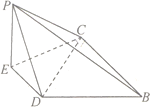
如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l1:2x﹣y+2=0与l2:x+y+4=0.
(1)若一条光线从l1与l2的交点射出,与x轴交于点P(3,0),且经x轴反射,求反射光线所在直线的方程;
(2)若直线l经过点P(3,0),且它夹在直线l1与l2之间的线段恰被点P平分,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com