
科目: 来源: 题型:
【题目】命题![]() :函数
:函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 上;命题
上;命题![]() :函数
:函数![]() 有极值.若命题
有极值.若命题![]() ,
,![]() 为真命题的实数
为真命题的实数![]() 的取值集合分别记为
的取值集合分别记为![]() ,
,![]() .
.
(1)求集合![]() ,
,![]() ;
;
(2)若命题“![]() 且
且![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足x2﹣5x+6<0.
(1)若a=1,且p∧q为真命题,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如下表
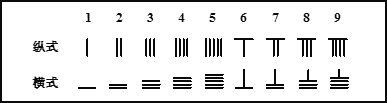
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推, 例如6613用算筹表示就是:![]() ,则26337用算筹可表示为( )
,则26337用算筹可表示为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,点M为BB1的中点.
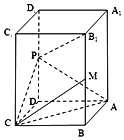
(1)求证:PB1⊥平面PAC;
(2)求直线CM与平面PAC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(III)设函数![]() ,
, ![]() ,过点
,过点![]() 作函数
作函数![]() 的图象的所有切线,令各切点的横坐标按从小到大构成数列
的图象的所有切线,令各切点的横坐标按从小到大构成数列![]() ,求数列
,求数列![]() 的所有项之和的值.
的所有项之和的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .已知以
.已知以![]() 为圆心,半径为4的圆与
为圆心,半径为4的圆与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 是该圆与抛物线
是该圆与抛物线![]() 的一个交点,
的一个交点,![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() 的纵坐标为
的纵坐标为![]() 且在
且在![]() 上,
上,![]() 、
、![]() 是
是![]() 上异于点
上异于点![]() 的另两点,且满足直线
的另两点,且满足直线![]() 和直线
和直线![]() 的斜率之和为
的斜率之和为![]() ,试问直线
,试问直线![]() 是否经过一定点,若是,求出定点的坐标,否则,请说明理由.
是否经过一定点,若是,求出定点的坐标,否则,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取![]() 名同学(男
名同学(男![]() 女
女![]() ),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 |
|
|
|
女同学 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在![]() 分钟,乙每次解答一道几何题所用的时间在
分钟,乙每次解答一道几何题所用的时间在![]() 分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何的![]() 名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为
名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com