【题目】一袋中有大小相同的4个红球和2个白球，给出下列结论：①从中任取3球，恰有一个白球的概率是；②从中有放回的取球6次，每次任取一球，恰好有两次白球的概率为；③现从中不放回的取球2次，每次任取1球，则在第一次取到红球后，第二次再次取到红球的概率为；④从中有放回的取球3次，每次任取一球，则至少有一次取到红球的概率为. 则其中正确命题的序号是（ ）

A.①B.②C.③D.④

【题目】已知，函数.

（1）若函数在上单调递增，求a的取值范围；

（2）用反证法证明：函数不可能为上的单调函数.

【题目】《周髀算经》中给出了弦图，所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形，若图中直角三角形两锐角分别为，，且小正方形与大正方形面积之比为，则的值为（ ）

A. B. C. D.

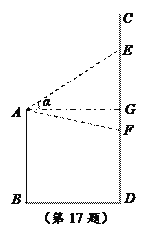
【题目】如图，某企业的两座建筑物AB，CD的高度分别为20m和40m，其底部BD之间距离为20m．为响应创建文明城市号召，进行亮化改造，现欲在建筑物AB的顶部A处安装一投影设备，投影到建筑物CD上形成投影幕墙，既达到亮化目的又可以进行广告宣传．已知投影设备的投影张角∠EAF为，投影幕墙的高度EF越小，投影的图像越清晰．设投影光线的上边沿AE与水平线AG所成角为α，幕墙的高度EF为y（m）．

（1）求y关于α的函数关系式，并求出定义域；

（2）当投影的图像最清晰时，求幕墙EF的高度．

【题目】某校学生会为了解该校学生对2017年全国两会的关注情况，随机调查了该校200名学生，并将这200名学生分为对两会“比较关注”与“不太关注”两类．已知这200名学生中男生比女生多20人，对两会“比较关注”的学生中男生人数与女生人数之比为，对两会“不太关注”的学生中男生比女生少5人．

（1）根据题意建立列联表，并判断是否有的把握认为男生与女生对两会的关注有差异？

（2）该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样，从中抽取7人，再从这7人中随机选出2人进行回访，求这2人全是男生的概率．

参考公式和数据：，其中．

(1)求数列{an}的通项公式与前n项和Sn；

(2)设Tn为数列{}的前n项和，问是否存在常数m，使Tn＝m[＋]，若存在，求m的值；若不存在，说明理由．

【题目】已知正数数列的前n项和为，满足，.

（1）求数列的通项公式，若恒成立，求k的范围；

（2）设，若是递增数列，求实数a的取值范围.

（1）可用线性回归模型拟合与之间的关系吗？如果能，请求出关于的线性回归方程，如果不能，请说明理由；

（2）公司决定再采购，两款车扩大市场，，两款车各100辆的资料如表：

平均每辆车每年可为公司带来收入500元，不考虑采购成本之外的其他成本，假设每辆车的使用寿命都是整数年，用每辆车使用寿命的频率作为概率，以每辆车产生利润的期望值作为决策依据，应选择采购哪款车型？

参考数据：，，，．

参考公式：相关系数；

回归直线方程，其中，．

【题目】已知函数，．

（1）讨论函数的单调性；

（2）设函数，若在上存在极值，求的取值范围，并判断极值的正负．

【题目】已知的三边长分别为a，b，c，其面积为S，则的内切圆O的半径.这是一道平面几何题，其证明方法采用“等面积法”设空间四面体四个面的面积分别为积为V，内切球半径为R.请用类比推理方法猜测对空间四面体存在类似结论为______.