
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的图象的相邻两条对称轴之间的距离为4,且有一个零点为
)的图象的相邻两条对称轴之间的距离为4,且有一个零点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】第七届世界军人运动会(7th CISM Military World Games) ,简称"武汉军运会”,于2019年10月18日至27日在中国武汉举行,共设置射击、游泳、田径篮球等27个大项、329个小项.来自100多个国家的近万名现役军人同台竞技.会议期间,某公司欲采购海南某水果种植基地的水果,公司王总经理与该种植基地的负责人张老板商定一次性采购一种水果的采购价![]() (千元/吨)与采购量
(千元/吨)与采购量![]() (吨)之间的函数关系的图象如图中的折线
(吨)之间的函数关系的图象如图中的折线![]() 所示(不包含端点
所示(不包含端点![]() ,但包含端点
,但包含端点![]() ).
).

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知该水果种植基地种植该水果的成本是8千元/吨,那么王总经理的采购量为多少时,该水果基地在这次买卖中所获得利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 轴上的点.
轴上的点.
(1)过点![]() 作直线
作直线![]() 与
与![]() 相切,求切线
相切,求切线![]() 的方程;
的方程;
(2)如果存在过点![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,且直线
两点,且直线![]() 与
与![]() 的倾斜角互补,求实数
的倾斜角互补,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨, ![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量, ![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(Ⅰ)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小;
的平均数与中位数的大小;
(Ⅱ)根据直方图估计利润![]() 不少于57万元的概率.
不少于57万元的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车、其他新能源汽车等.它是未来汽车的发展方向.一个新能源汽车制造厂引进了一条新能源汽车整车装配流水线,这条流水线生产的新能源汽车数量![]() (辆)与创造的价值
(辆)与创造的价值![]() (万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
(万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》卷五《商功》中有如下叙述“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈“刍甍”指的是底面为矩形的对称型屋脊状的几何体,“下广三丈”是指底面矩形宽三丈,“袤四丈”是指底面矩形长四丈,“上袤二丈”是指脊长二丈,“无宽”是指脊无宽度,“高一丈”是指几何体的高为一丈.现有一个刍甍如图所示,下广三丈,袤四丈,上袤三丈,无广,高二丈,则该刍甍的外接球的表面积为_______________平方丈.
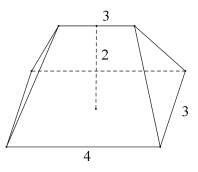
查看答案和解析>>
科目: 来源: 题型:
【题目】某手机企业为确定下一年度投入某种产品的研发费用,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 千万元与年销售量
千万元与年销售量![]() 千万件的数据,得到散点图1,对数据作出如下处理:令
千万件的数据,得到散点图1,对数据作出如下处理:令![]() ,
,![]() ,得到相关统计量的值如图2:
,得到相关统计量的值如图2:

(1)利用散点图判断![]() 和
和![]()
![]() 哪一个更适合作为年研发费用
哪一个更适合作为年研发费用![]() 和年销售量
和年销售量![]() 的回归类型(不必说明理由),并根据数据,求出
的回归类型(不必说明理由),并根据数据,求出![]() 与
与![]() 的回归方程;
的回归方程;
(2)已知企业年利润![]() 千万元与
千万元与![]() 的关系式为
的关系式为![]() (其中
(其中![]() 为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()
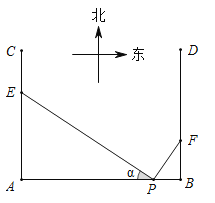
![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com