
科目: 来源: 题型:
【题目】我国是水资源匮乏国家,节约用水是每个中国公民应有的意识.为了保护水资源,提倡节约用水,某城市对居民生活用水实行“阶梯水价”,计费方法如下表:
每户每月用水量 | 水价 |
不超过12 | 3元/ |
超过12 | 6元/ |
超过18 | 9元/ |
(1)该城市居民小张家月用水量记为![]() ,应交纳水费y(元),试建立y与x的函数解析式,并作出其图像;
,应交纳水费y(元),试建立y与x的函数解析式,并作出其图像;
(2)若小张家十月份交纳水费90元,求他家十月份的用水量.
查看答案和解析>>
科目: 来源: 题型:
【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).

(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
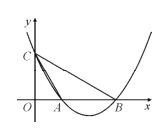
【题目】如图,二次函数![]() 的图像与x轴交于
的图像与x轴交于![]() 和
和![]() ,与y轴交于C点,且
,与y轴交于C点,且![]() 是等腰三角形.
是等腰三角形.
(1)求![]() 的解析式;
的解析式;
(2)在A、B之间的抛物线段上是否存在异于A、B的点D,使![]() 与
与![]() 的面积相等?若存在,求D点的坐标,若不存在,说明理由.
的面积相等?若存在,求D点的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() ,且
,且![]() .
.
(1)求函数![]() ,
,![]() 的解析式;
的解析式;
(2)设函数 ,记
,记![]() (
(![]() ,
,![]() ).探究是否存在正整数
).探究是否存在正整数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 恒成立?若存在,求出所有满足条件的正整数
恒成立?若存在,求出所有满足条件的正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考结论:设![]() 均为常数,函数
均为常数,函数![]() 的图象关于点
的图象关于点![]() 对称的充要条件是
对称的充要条件是![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了测量某塔的高度,某人在一条水平公路![]() 两点进行测量.在
两点进行测量.在![]() 点测得塔底
点测得塔底![]() 在南偏西
在南偏西![]() ,塔顶仰角为
,塔顶仰角为![]() ,此人沿着南偏东
,此人沿着南偏东![]() 方向前进10米到
方向前进10米到![]() 点,测得塔顶的仰角为
点,测得塔顶的仰角为![]() ,则塔的高度为( )
,则塔的高度为( )
A. 5米B. 10米C. 15米D. 20米
查看答案和解析>>
科目: 来源: 题型:
【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的![]() ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上奇函数
上奇函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式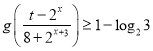 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() :
:![]() 与直线
与直线![]() :
:![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.

(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,点M是PQ的中点,直线
两点,点M是PQ的中点,直线![]() 与直线
与直线![]() 相交于点N.探索
相交于点N.探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com