
科目: 来源: 题型:
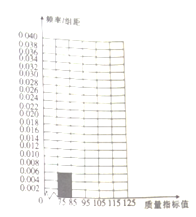
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;
(2)估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |
查看答案和解析>>
科目: 来源: 题型:
【题目】袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到“和”“平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
232 321 230 023 123 021 132 220 011 203 331 100
231 130 133 231 031 320 122 103 233 221 020 132
由此可以估计,恰好第三次就停止的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市理论预测2020年到2024年人口总数与年份的关系如下表所示:
年份202x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请在右面的坐标系中画出上表数据的散点图;
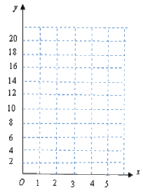
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)据此估计2025年该城市人口总数.
(参考公式: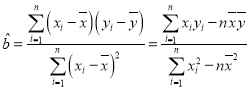 ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 与函数
与函数![]() 表示同一个函数;
表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③函数![]() 的图象可由
的图象可由![]() 的图象向右平移1个单位得到;
的图象向右平移1个单位得到;
④若函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() ;
;
⑤设函数![]() 是在区间
是在区间![]() 上图象连续的函数,且
上图象连续的函数,且![]() ,则方程
,则方程![]() 在区间
在区间![]() 上至少有一实根.
上至少有一实根.
其中正确命题的序号是________.(填上所有正确命题的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】一个袋子里装有7个球,其中有红球4个.白球3个.这些球除颜色外全相同.
(1)若一次从袋中取出3个球,取出的球颜色不完全相同的概率;
(2)若一次从袋中取出3个球.其中若取到红球得0分,取到白球得1分,记随机变量![]() 为取出的三个小球得分之和,求
为取出的三个小球得分之和,求![]() 的分布列,并求其数学期望.
的分布列,并求其数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() ,点
,点![]() 为
为![]() 的焦点,过
的焦点,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点.
两点.
(1)设![]() ,
,![]() 在
在![]() 的准线上的射影分别为
的准线上的射影分别为![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:
,证明:![]() .
.
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之和为定值?若存在,求出点
的斜率之和为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了缓解市民吃肉难的生活问题,某生猪养殖公司欲将一批猪肉用冷藏汽车从甲地运往相距![]() 千米的乙地,运费为每小时
千米的乙地,运费为每小时![]() 元,装卸费为
元,装卸费为![]() 元,猪肉在运输途中的损耗费(单位:元)是汽车速
元,猪肉在运输途中的损耗费(单位:元)是汽车速![]() 度值的
度值的![]() 倍.(说明:运输的总费用=运费+装卸费+损耗费)
倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)若汽车的速度为每小时![]() 千米,试求运输的总费用;
千米,试求运输的总费用;
(2)为使运输的总费用不超过![]() 元,求汽车行驶速度的范围;
元,求汽车行驶速度的范围;
(3)若要使运输的总费用最小,汽车应以每小时多少千米的速度行驶?
查看答案和解析>>
科目: 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com