【题目】在单位正内任取一点P，以PA、PB、PC为边生成．

（1）当分别为锐角三角形、直角三角形、钝角三角形时，求出点P的轨迹．

（2）证明：当的周长取最小值时，面积取最大值．

A.，，B.，，

C.，，D.，，

【题目】在平面直角坐标系中,已知直线的参数方程为（为参数）.在以坐标原点为极点,轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线的极坐标方程是.

（1）求直线的普通方程与曲线的直角坐标方程；

（2）设点.若直与曲线相交于两点,求的值.

【题目】已知函数.

（1）当时,讨论函数的单调性；

（2）当时,若不等式在时恒成立,求实数的取值范围.

【题目】某社区为了了解青少年的身体素质，对本社区的名青少年进行了调研，随机抽取了若干名，年龄全部介于与岁之间，将年龄按如下方式分成五组：第一组；第二组；；第五组．按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三个组的频率之比为，且第二组的频数为．

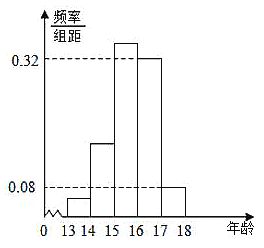
（1）试估计这名青少年中年龄在内的人数；

（2）求从本社区的名青少年中随机抽取出的调研人数．

【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值与销售单价之间的关系,经统计得到如下数据：

（1）已知销售单价与等级代码数值之间存在线性相关关系,求关于的线性回归方程(系数精确到0.1)；

（2）若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98，请估计该等级的中国小龙虾销售单价为多少元？

参考公式：对一组数据,，····,其回归直线的斜率和截距最小二乘估计分别为：,.

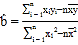参考数据：,.

【题目】如图,四棱锥的底面是边长为2的菱形,,平面,点是棱的中点.

（1）证明：平面；

（2）当时,求三棱锥的体积.

【题目】从、、、这个数中一次随机地取个数，记所取的这个数的和为，则下列说法错误的是（ ）

A.事件“”的概率为

B.事件“”的概率为

C.事件“”与事件“”为互斥事件

D.事件“”与事件“”互为对立事件

设函数

（1）若在处取得极值，确定的值，并求此时曲线在点处的切线方程；

（2）若在上为减函数，求的取值范围。