
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 的线性回归直线方程为
的线性回归直线方程为![]() ,且
,且![]() ,
,![]() 之间的一组相关数据如下表所示,则下列说法错误的为
之间的一组相关数据如下表所示,则下列说法错误的为

A.变量![]() ,
,![]() 之间呈现正相关关系B.可以预测,当
之间呈现正相关关系B.可以预测,当![]() 时,
时,![]()
C.![]() D.由表格数据可知,该回归直线必过点
D.由表格数据可知,该回归直线必过点![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】BMI指数(身体质量指数,英文为Body Mass Index,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方. 根据中国肥胖问题工作组标准,当BMI![]() 时为肥胖. 某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,得到被调查者的频率分布直方图如图:
时为肥胖. 某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,得到被调查者的频率分布直方图如图:

(1)求被调查者中肥胖人群的BMI 平均值![]() ;
;
(2)根据频率分布直方图,完成下面的![]() 列联表,并判断能有多大(百分数)的把握认为 35 岁以上成人高血压与肥胖有关?
列联表,并判断能有多大(百分数)的把握认为 35 岁以上成人高血压与肥胖有关?
肥胖 | 不肥胖 | 总计 | |
高血压 | |||
非高血压 | |||
总计 |
参考公式: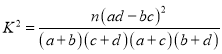 ,其中
,其中![]() .
.
参考数据:
| 0.25 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)
已知函数![]() 是奇函数,
是奇函数,![]() 的定义域为
的定义域为![]() .当
.当![]() 时,
时,![]()
![]() .(e为自然对数的底数).
.(e为自然对数的底数).
(1)若函数![]() 在区间
在区间![]() 上存在极值点,求实数
上存在极值点,求实数![]() 的取值范围;
的取值范围;
(2)如果当x≥1时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过点P作圆
,点P在直线l上,过点P作圆![]() 的切线PA,PB,切点为A,B.
的切线PA,PB,切点为A,B.
(1)若![]() ,求点P的坐标;
,求点P的坐标;
(2)求证:经过A,P,![]() 三点的圆必经过异于
三点的圆必经过异于![]() 的某个定点,并求该定点的坐标.
的某个定点,并求该定点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某网红直播平台为确定下一季度的广告投入计划,收集了近6个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
广告投入量/万元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/万元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
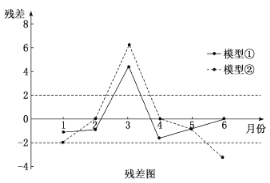
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由.
(2)残差绝对值大于2的数据被认为是异常数据,需要剔除:
(i)剔除的异常数据是哪一组?
(ii)剔除异常数据后,求出(1)中所选模型的回归方程;
(iii)广告投入量![]() 时,(ii)中所得模型收益的预报值是多少?
时,(ii)中所得模型收益的预报值是多少?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: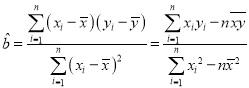 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】经统计,某校学生上学路程所需要时间全部介于![]() 与
与![]() 之间(单位:分钟).现从在校学生中随机抽取
之间(单位:分钟).现从在校学生中随机抽取![]() 人,按上学所学时间分组如下:第
人,按上学所学时间分组如下:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得打如图所示的频率分布直方图.
,得打如图所示的频率分布直方图.
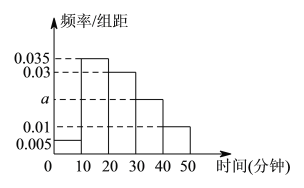
(Ⅰ)根据图中数据求![]() 的值.
的值.
(Ⅱ)若从第![]() ,
,![]() ,
,![]() 组中用分成抽样的方法抽取
组中用分成抽样的方法抽取![]() 人参与交通安全问卷调查,应从这三组中各抽取几人?
人参与交通安全问卷调查,应从这三组中各抽取几人?
(Ⅲ)在(Ⅱ)的条件下,若从这![]() 人中随机抽取
人中随机抽取![]() 人参加交通安全宣传活动,求第
人参加交通安全宣传活动,求第![]() 组至少有
组至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题错误的是
A. 三棱锥的四个面可以都是直角三角形;
B. 等差数列{an}的前n项和为Sn(n=1,2,3…),若当首项a1和公差d变化时,a5+a8+a11是一个定值,则S16为定值;
C. ![]() 中,sinA>sinB是
中,sinA>sinB是![]() 的充要条件;
的充要条件;
D. 若双曲线的渐近线互相垂直,则这条双曲线是等轴双曲线.
查看答案和解析>>
科目: 来源: 题型:
【题目】设自然数![]() 。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当
。求证:全体不大于n的合数可重新排列(不一定按原来的大小顺序排列),使得每三个依次相邻的数都有大于1的公因数(例如,当![]() 时,排列
时,排列![]() 就满足要求)。
就满足要求)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com