
科目: 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2020年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
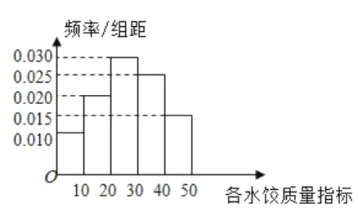
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,–2),C(4,1).
(1)若![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量![]() ,
,![]() ,若k
,若k![]() –
–![]() 与
与![]() +3
+3![]() 平行,求实数
平行,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过![]() 的前提下认为喜好体育运动与性别有关?说明你的理由.
的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式: ![]() )
)
临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,三国时代数学家赵爽在《周髀算经》中利用弦图,给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形(阴影),设直角三角形有一内角为![]() ,若向弦图内随机抛掷500颗米粒(大小忽略不计,取
,若向弦图内随机抛掷500颗米粒(大小忽略不计,取![]() ),则落在小正方形(阴影)内的米粒数大约为( )
),则落在小正方形(阴影)内的米粒数大约为( )
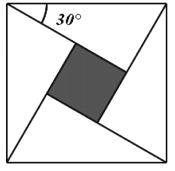
A. 134 B. 67 C. 200 D. 250
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,使
,使![]() 是等边三角形且面积为
是等边三角形且面积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 是圆
是圆![]() 与抛物线
与抛物线![]() 的一个交点,点
的一个交点,点![]() ,当
,当![]() 取得最小值时,求此时圆
取得最小值时,求此时圆![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市正在创建全国文明城市,某高中为了解学生的创文知晓率,按分层抽样的方法从“表演社”、“演讲社”、“围棋社”三个活动小组中随机抽取了6人进行问卷调查,各活动小组人数统计如下图:
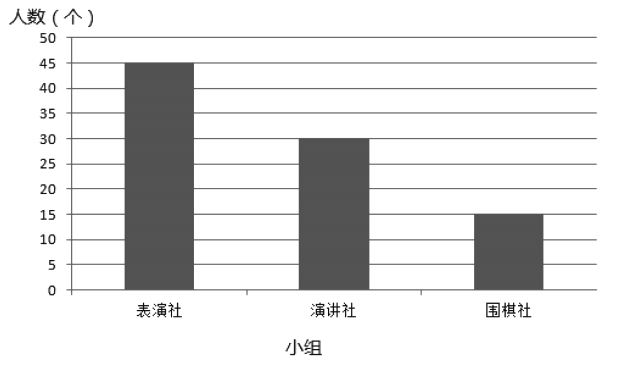

(1)从参加问卷调查的6名学生中随机抽取2名,求这2名学生来自同一小组的概率;
(2)从参加问卷调查的6名学生中随机抽取3名,用![]() 表示抽得“表演社”小组的学生人数,求
表示抽得“表演社”小组的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com