
科目: 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率;先由计算器给出0到9之间取整数值的随机数,指定0、1、2表示没有击中目标,3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20随机数:![]()
![]()
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
A.0.55B.0.6C.0.65D.0.7
查看答案和解析>>
科目: 来源: 题型:
【题目】临川一中实验学校坐落在抚州火车站附近,在校区东边(如图),有一直径为8米的半圆形空地,现计划移植一古树,但需要有辅助光照.半圆周上的![]() 处恰有一可旋转光源满足古树生长的需要,该光源照射范围是
处恰有一可旋转光源满足古树生长的需要,该光源照射范围是![]() ,点
,点![]() 在直径
在直径![]() 上,且
上,且![]() .
.
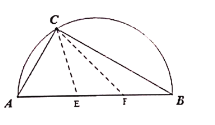
(1)若![]() ,求
,求![]() 的长;
的长;
(2)设![]() ,求该空地种植古树的最大面积.
,求该空地种植古树的最大面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人射击,已知甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() .
.
(1)两人各射击一次,求至少有一人击中目标的概率;
(2)若制定规则如下:两人轮流射击,每人至多射击2次,甲先射,若有人击中目标即停止射击.
①求乙射击次数不超过1次的概率;
②记甲、乙两人射击次数和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位响应党中央“精准扶贫”号召,对某村6户贫困户中的甲户进行定点帮扶,每年跟踪调查统计一次,从2015年1月1日至2018年12月底统计数据如下(人均年纯收入):
年份 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 |
收入 | 25 | 28 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
(2)2019年初,根据扶贫办的统计知,该村剩余5户贫困户中还有2户没有脱贫,现从这5户中抽取2户,求至少有一户没有脱贫的概率.
参考公式: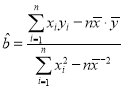 ,
,![]() ,其中
,其中![]() ,
,![]() 为数
为数![]() ,
,![]() 的平均数.
的平均数.
查看答案和解析>>
科目: 来源: 题型:
【题目】有限集合S中元素的个数记做![]() ,设A,B都为有限集合,给出下列命题:
,设A,B都为有限集合,给出下列命题:
①![]() 的充要条件是
的充要条件是![]()
②![]() 的必要不充分条件是
的必要不充分条件是![]()
③![]() 的充分不必要条件是
的充分不必要条件是![]()
④![]() 的充要条件是
的充要条件是![]()
其中,真命题有( )
A.①②③B.①②C.②③D.①④
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2015年1月至2017年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()
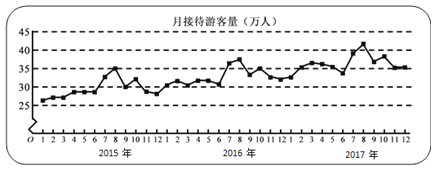
A. 年接待游客量逐年增加
B. 各年的月接待游客量高峰期在8月
C. 2015年1月至12月月接待游客量的中位数为30万人
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com