
科目: 来源: 题型:
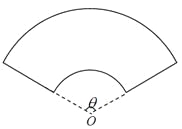
【题目】某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目: 来源: 题型:
【题目】若数列![]() 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有![]() 成立,则称数列
成立,则称数列![]() 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列![]() 满足
满足![]() ,
, ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.若![]() ,则m可以取3个不同的值;
,则m可以取3个不同的值;
B.若![]() ,则数列
,则数列![]() 是周期为3的数列;
是周期为3的数列;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列
的数列
D.存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列
是周期数列
查看答案和解析>>
科目: 来源: 题型:
【题目】《情境》刘晓红同学在做达标训练的课外作业时,遇到一个如何用五点法作出正弦型函数在长度为一个周期的闭区间上的图象及图象之间如何进行变换的问题,她犯愁了.
《问题》设函数![]() 的周期为
的周期为![]() ,且图象过点
,且图象过点![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)用五点法作函数![]() 在长度为一个周期的闭区间上的图象;
在长度为一个周期的闭区间上的图象;
(3)叙述函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
由于刘晓红对上述问题还没有掌握解决方法及解题概念和步骤,导致无从下手,于是她请教了班上的学习委员张倩同学给她做了如下点拨:
用五点法作出在一个周期的闭区间上的图象,首先要列表并分别令相位![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,再解出对应的
,再解出对应的![]() 、
、![]() 的值,得出坐标
的值,得出坐标![]() ,然后描点,最后画出图象.而由函数
,然后描点,最后画出图象.而由函数![]() 的图象变到函数
的图象变到函数![]() 的图象主要有两种途径:①按物理量初相
的图象主要有两种途径:①按物理量初相![]() ,周期
,周期![]() ,振幅
,振幅![]() 的顺序变换;②按物理量周期
的顺序变换;②按物理量周期![]() ,初相
,初相![]() ,振幅
,振幅![]() 的顺序变换.要注意两者操作的区别,防止出错.
的顺序变换.要注意两者操作的区别,防止出错.
经过张倩耐心而细致的解释,刘晓红豁然开朗,并对该题解答如下:
(注意:解答第(3)问时,要按照题中要求,写出两种变换过程)
查看答案和解析>>
科目: 来源: 题型:
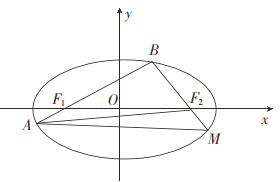
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.
(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良后所排放的废气中含有的污染物数量为
,首次改良后所排放的废气中含有的污染物数量为![]() .设改良工艺前所排放的废气中含有的污染物数量为
.设改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良工艺后所排放的废气中含有的污染物数量为
,首次改良工艺后所排放的废气中含有的污染物数量为![]() ,则第
,则第![]() 次改良后所排放的废气中的污染物数量
次改良后所排放的废气中的污染物数量![]() ,可由函数模型
,可由函数模型![]() 给出,其中
给出,其中![]() 是指改良工艺的次数.
是指改良工艺的次数.
(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过![]() ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取
,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某校举行了一次考试,从学生中随机选取了![]() 人的成绩作为样本进行统计.已知这些学生的成绩全部在
人的成绩作为样本进行统计.已知这些学生的成绩全部在![]() 分至
分至![]() 分之间,现将成绩按如下方式分成
分之间,现将成绩按如下方式分成![]() 组:第一组
组:第一组![]() ,第二组
,第二组![]() ,.......,第六组
,.......,第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
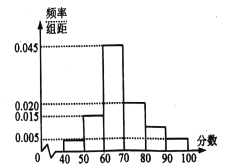
(1)估计这次月考数学成绩的平均分和众数;
(2)从成绩大于等于![]() 分的学生中随机抽取
分的学生中随机抽取![]() 人,求至少有
人,求至少有![]() 名学生的成绩在
名学生的成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com