
科目: 来源: 题型:
【题目】设有编号为1,2,3,4,5的五把锁和对应的五把钥匙.现给这5把钥匙也贴上编号为1,2,3,4,5的五个标签,则共有______种不同的贴标签的方法:若想使这5把钥匙中至少有2把能打开贴有相同标签的锁,则有______种不同的贴标签的方法.(本题两个空均用数字作答)
查看答案和解析>>
科目: 来源: 题型:
【题目】小明口袋中有3张10元,3张20元(因纸币有编号认定每张纸币不同),现从中掏出纸币超过45元的方法有_______种;若小明每次掏出纸币的概率是等可能的,不放回地掏出4张,刚好是50元的概率为_______.
查看答案和解析>>
科目: 来源: 题型:
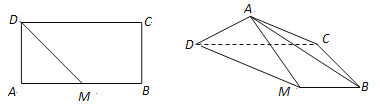
【题目】如图,在矩形ABCD中,AB=2,AD=1,M为AB的中点,将△ADM沿DM翻折.在翻折过程中,当二面角A—BC—D的平面角最大时,其正切值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C:![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点Q在直线![]() 上,且
上,且![]() 。证明:过点P且垂直于OQ的直线l过C的左焦点F.
。证明:过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的短轴长为4,离心率为
的短轴长为4,离心率为![]() ,斜率不为0的直线l与椭圆恒交于A,B两点,且以AB为直径的圆过椭圆的右顶点M.
,斜率不为0的直线l与椭圆恒交于A,B两点,且以AB为直径的圆过椭圆的右顶点M.
(1)求椭圆的标准方程;
(2)直线l是否过定点,如果过定点,求出该定点的坐标;如果不过定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,在高三年级中随机选取![]() 名学生进行跟踪问卷,其中每周线上学习数学时间不少于
名学生进行跟踪问卷,其中每周线上学习数学时间不少于![]() 小时的有
小时的有![]() 人,在这
人,在这![]() 人中分数不足
人中分数不足![]() 分的有
分的有![]() 人;在每周线上学习数学时间不足于
人;在每周线上学习数学时间不足于![]() 小时的人中,在检测考试中数学平均成绩不足
小时的人中,在检测考试中数学平均成绩不足![]() 分的占
分的占![]() .
.
(1)请完成![]() 列联表;并判断是否有
列联表;并判断是否有![]() 的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
分数不少于 | 分数不足 | 合计 | |
线上学习时间不少于 | |||
线上学习时间不足 | |||
合计 |
(2)在上述样本中从分数不足于![]() 分的学生中,按照分层抽样的方法,抽到线上学习时间不少于
分的学生中,按照分层抽样的方法,抽到线上学习时间不少于![]() 小时和线上学习时间不足
小时和线上学习时间不足![]() 小时的学生共
小时的学生共![]() 名,若在这
名,若在这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求这
人,求这![]() 人每周线上学习时间都不足
人每周线上学习时间都不足![]() 小时的概率.(临界值表仅供参考)
小时的概率.(临界值表仅供参考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式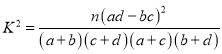 ,其中
,其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量![]() (单位:瓶)为多少时?
(单位:瓶)为多少时?![]() 的数学期望达到最大值?
的数学期望达到最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com