【题目】已知椭圆过点P（2，1）．

（1）求椭圆C的方程，并求其离心率；

（2）过点P作x轴的垂线l，设点A为第四象限内一点且在椭圆C上（点A不在直线l上），点A关于l的对称点为A'，直线A'P与C交于另一点B．设O为原点，判断直线AB与直线OP的位置关系，并说明理由．

【题目】（本题16分）某乡镇为了进行美丽乡村建设，规划在长为10千米的河流OC的一侧建一条观光带，观光带的前一部分为曲线段OAB，设曲线段OAB为函数，（单位：千米）的图象，且曲线段的顶点为；观光带的后一部分为线段BC，如图所示.

（1）求曲线段OABC对应的函数的解析式；

（2）若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ，绿化带由线段MQ，QP， PN构成，其中点P在线段BC上．当OM长为多少时，绿化带的总长度最长？

【题目】手机作为客户端越来越为人们所青睐，通过手机实现衣食住行消费已经成为一种主要的消费方式.在某市，随机调查了200名顾客购物时使用手机支付的情况，得到如下的2×2列联表，已知从使用手机支付的人群中随机抽取1人，抽到青年的概率为.

（I）根据已知条件完成2×2列联表，并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”？

2×2列联表：

（Ⅱ）现采用分层抽样的方法从这200名顾客中按照“使用手机支付”和“不使用手机支付”抽取一个容量为10的样本，再从中随机抽取3人，求这三人中“使用手机支付”的人数的分布列及期望.

附：

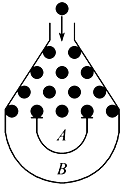
【题目】某超市春节大酬宾，购物满100元可参加一次抽奖活动，规则如下：顾客将一个半径适当的小球放入如图所示的容器正上方的人口处，小球在自由落下的过程中，将3次遇到黑色障碍物，最后落入A袋或B袋中，顾客相应获得袋子里的奖品.已知小球每次遇到黑色障碍物时，向左向右下落的概率都为.若活动当天小明在该超市购物消费108元，按照活动规则，他可参加一次抽奖，则小明获得A袋中的奖品的概率为_____.

【题目】已知函数．

（1）当时，求曲线在点处的切线方程；

（2）当时，若曲线在直线的上方，求实数的取值范围．

【题目】已知定义在R上的函数满足：（1）；（2）；（3）时，.则大小关系

A. B.

C. D.

【题目】如图1，在四边形ABCD中，AD∥BC，BC=2AD，E，F分别为AD，BC的中点，AE=EF，．将四边形ABFE沿EF折起，使平面ABFE⊥平面EFCD（如图2），G是BF的中点．

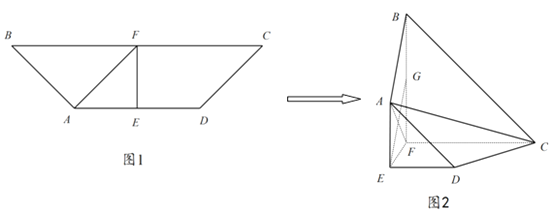
（1）证明：AC⊥EG；

（2）在线段BC上是否存在一点H，使得DH∥平面ABFE？若存在，求的值；若不存在，说明理由；

（3）求二面角D-AC-F的大小．

A.对于任意一个圆，其“优美函数”有无数个

B.可以是某个圆的“优美函数”

C.正弦函数可以同时是无数个圆的“优美函数”

D.函数是“优美函数”的充要条件为函数的图象是中心对称图形

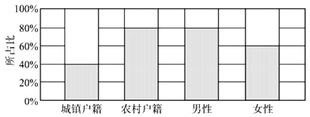
A.是否倾向选择生育二胎与户籍有关

B.是否倾向选择生育二胎与性别有关

C.调查样本里面倾向选择生育二胎的人群中，男性人数少于女性人数

D.倾向选择不生育二胎的人群中，农村户籍人数多于城镇户籍人数

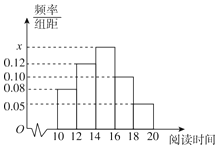
（1）求频率分布直方图中的x的值；

（2）试估计该校所有学生中，课外阅读时间不小于16小时的学生人数；

（3）已知课外阅读时间在[10，12）的样本学生中有3名女生，现从阅读时间在[10，12）的样本学生中随机抽取3人，记X为抽到女生的人数，求X的分布列与数学期望E（X）．