
科目: 来源: 题型:
【题目】为了调查某品牌饮料的某种食品添加剂是否超标,现对该品牌下的两种饮料一种是碳酸饮料![]() 含二氧化碳
含二氧化碳![]() ,另一种是果汁饮料
,另一种是果汁饮料![]() 不含二氧化碳
不含二氧化碳![]() 进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶
进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶![]() 均是
均是![]() 组成的一个样本,进行了检测,得到了如下茎叶图
组成的一个样本,进行了检测,得到了如下茎叶图![]() 根据国家食品安全规定当该种添加剂的指标大于
根据国家食品安全规定当该种添加剂的指标大于![]() 毫克
毫克![]() 为偏高,反之即为正常.
为偏高,反之即为正常.
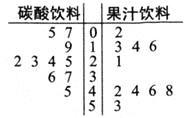
(1)依据上述样本数据,完成下列![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
正常 | 偏高 | 合计 | |
碳酸饮料 | |||
果汁饮料 | |||
合计 |
(2)现从食品添加剂偏高的样本中随机抽取2瓶饮料去做其它检测,求这两种饮料都被抽到的概率.
参考公式: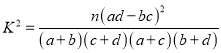 ,其中
,其中![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
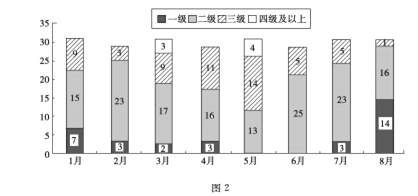
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)在极坐标系中,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() ,求直线
,求直线![]() 的极坐标方程.
的极坐标方程.
(2)已知直线![]()
![]() (
(![]() 为参数)恒经过椭圆
为参数)恒经过椭圆![]()
![]() (
(![]() 为参数)的右焦点
为参数)的右焦点![]() .
.
①求![]() 的值;
的值;
②设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.(
的取值范围.(![]() 是自然对数的底数,
是自然对数的底数,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求证:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 中是否存在不同的三项按照一定顺序重新排列后,构成等差数列?若存在,求满足条件的项;若不存在,说明理由.
中是否存在不同的三项按照一定顺序重新排列后,构成等差数列?若存在,求满足条件的项;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.己知
轴的非负半轴为极轴建立极坐标系.己知
点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为,
的参数方程为,![]() (
(![]() 为参数).曲线
为参数).曲线![]() 和曲线
和曲线![]() 相交于
相交于![]() 两点.
两点.
(1)求点![]() 的直角坐标;
的直角坐标;
(2)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(3)求![]() 的面枳
的面枳![]() ,
,
查看答案和解析>>
科目: 来源: 题型:
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
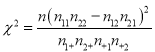
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com