
科目: 来源: 题型:
【题目】已知![]() ,抛物线
,抛物线![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 异于原点
异于原点![]() 的交点为
的交点为![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ;
;
(2)证明: ![]() 的面积与四边形
的面积与四边形![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广.某网游经销商在甲地区![]() 个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
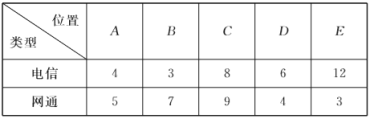
(Ⅰ)如果在测试中掉线次数超过![]() 次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过
次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过![]() 的前提下,能否说明网络状况与网络的类型有关?
的前提下,能否说明网络状况与网络的类型有关?
(Ⅱ)若该游戏经销商要在上述接受测试的电信的![]() 个地区中任选
个地区中任选![]() 个作为游戏推广,求
个作为游戏推广,求![]() 、
、![]() 两地区至少选到一个的概率.
两地区至少选到一个的概率.
参考公式:![]()

查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与直线
与直线![]() 平行,且过坐标原点,圆
平行,且过坐标原点,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 和圆
和圆![]() 相交于点
相交于点![]() 、
、![]() 两点,求
两点,求![]() 的周长.
的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】现将甲、乙两个学生在高二的6次数学测试的成绩(百分制)制成如图所示的茎叶图,进入高三后,由于改进了学习方法,甲、乙这两个学生的考试成绩预计同时有了大的提升:若甲(乙)的高二任意一次考试成绩为![]() ,则甲(乙)的高三对应的考试成绩预计为
,则甲(乙)的高三对应的考试成绩预计为![]() .
.

(1)试预测:高三6次测试后,甲、乙两个学生的平均成绩分别为多少?谁的成绩更稳定?
(2)若已知甲、乙两个学生的高二6次考试成绩分别由低到高进步的,定义![]() 为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求
为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求![]() 的平均值.
的平均值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() ,以
,以![]() 为边在轴上方作一个平行四边形
为边在轴上方作一个平行四边形![]() ,满足
,满足![]() .
.
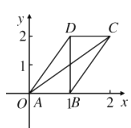
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)将动点![]() 的轨迹方程所表示的曲线
的轨迹方程所表示的曲线![]() 向左平移
向左平移![]() 个单位得曲线,若
个单位得曲线,若![]() 是曲线
是曲线![]() 上的一点,当
上的一点,当 时,记
时,记![]() 为点
为点![]() 到直线
到直线![]() 距离的最大值,求
距离的最大值,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,(如图所示),表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位、百位、万位数用纵式表示,十位、千位、十万位用横式表示,以此类推.例如8455用算筹表示就是![]() ,则以下用算筹表示的四位数正确的为( )
,则以下用算筹表示的四位数正确的为( )
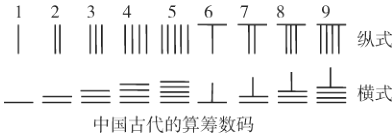
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是正方形,G是线段AD延长线一点,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,F是线段PG的中点;
,F是线段PG的中点;

![]() 求证:
求证:![]() 平面PAC;
平面PAC;
![]() 若
若![]() 时,求平面PCF与平面PAG所成二面角的余弦值.
时,求平面PCF与平面PAG所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com