【题目】南北朝时期的伟大数学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”.其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等.如图，夹在两个平行平面之间的两个几何体的体积分别为、，被平行于这两个平面的任意平面截得的两个截面面积分别为、，则命题：“、相等”是命题“、总相等”的（ ）

A.充分不必要条件B.必要不充分条件

C.充要条件D.既不充分也不必要条件

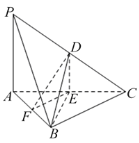
A.三棱锥D-BEF的体积为6

B.直线PB与直线DF垂直

C.平面DEF截三棱锥P-ABC所得的截面面积为12

D.点P与点A到平面BDE的距离相等

【题目】在平面直角坐标系xOy中，将椭圆上每一点的横坐标保持不变，纵坐标变为原来的一半，得曲线C，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为．

写出曲线C的普通方程和直线l的直角坐标方程；

已知点且直线l与曲线C交于A、B两点，求的值．

【题目】已知函数在上是增函数．

求实数的值；

若函数有三个零点，求实数的取值范围．

【题目】已知函数的最大值为，其图像相邻的两条对称轴之间的距离为，且的图像关于点对称，则下列结论正确的是（ ）.

A.函数的图像关于直线对称

B.当时，函数的最小值为

C.若，则的值为

D.要得到函数的图像，只需要将的图像向右平移个单位

【题目】太极图被称为“中华第一图”，闪烁着中华文明进程的光辉，它是由黑白两个鱼形纹组成的图案，俗称阴阳鱼，太极图展现了一种相互转化，相对统一的和谐美.定义：能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”，设圆O：，则下列说法中正确的是( )

A.函数是圆O的一个太极函数

B.圆O的所有非常数函数的太极函数都不能为偶函数

C.函数是圆O的一个太极函数

D.函数的图象关于原点对称是为圆O的太极函数的充要条件

【题目】已知椭圆的方程为，离心率，且短轴长为4．

求椭圆的方程；

已知，，若直线l与圆相切，且交椭圆E于C、D两点，记的面积为，记的面积为，求的最大值．

【题目】已知三棱柱中，，，，．

求证：面面；

若，在线段上是否存在一点，使二面角的平面角的余弦值为？若存在，确定点的位置；若不存在，说明理由

【题目】2020年是中国传统的农历“鼠年”，有人用3个圆构成“卡通鼠”的形象，如图：是圆Q的圆心，圆Q过坐标原点O；点L、S均在x轴上，圆L与圆S的半径都等于2，圆S、圆L均与圆Q外切.已知直线l过点O.

（1）若直线l与圆L、圆S均相切，则l截圆Q所得弦长为__________；

（2）若直线l截圆L、圆S、圆Q所得弦长均等于d，则__________.

【题目】田忌赛马是史记中记载的一个故事，说的是齐国将军田忌经常与齐国众公子赛马，孙膑发也们的马脚力都差不多，都分为上、中、下三等于是孙膑给田忌将军制定了一个必胜策略：比赛即将开始时，他让田忌用下等马对战公子们的上等马，用上等马对战公子们的中等马，用中等马对战公子们的下等马，从而使田忌赢得公子们许多赌注假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示：

比赛规则规定：一次比由三场赛马组成，每场由公子和田忌各出一匹马出骞，结果只有胜和负两种，并且毎一方三场赛马的马的等级各不相同，三场比赛中至少获胜两场的一方为最终胜利者．

如果按孙膑的策略比赛一次，求田忌获胜的概率；

如果比赛约定，只能同等级马对战，每次比赛赌注1000金，即胜利者赢得对方1000金，每月比赛一次，求田忌一年赛马获利的数学期望．