
【题目】2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:![]() 是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.
是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.

(1)若直线l与圆L、圆S均相切,则l截圆Q所得弦长为__________;
(2)若直线l截圆L、圆S、圆Q所得弦长均等于d,则![]() __________.
__________.
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球.
(1)从盒中任取两球,求取出的球的编号之和大于5的概率.
(2)从盒中任取一球,记下该球的编号![]() ,将球放回,再从盒中任取一球,记下该球的编号
,将球放回,再从盒中任取一球,记下该球的编号![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() 的普通方程为
的普通方程为![]() ,以原点为极点,
,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,并取与直角坐标系相同的长度单位,建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,并取与直角坐标系相同的长度单位,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若点![]() 、
、![]() 分别在曲线
分别在曲线![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,D,E分别为AB,AC的中点,
中,D,E分别为AB,AC的中点,![]() ,以DE为折痕将
,以DE为折痕将![]() 折起,使点A到达点P的位置,如图.
折起,使点A到达点P的位置,如图.

(1)证明:![]() ;
;
(2)若平面DEP![]() 平面BCED,求直线DC与平面BCP所成角的正弦值。
平面BCED,求直线DC与平面BCP所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: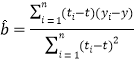 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com