【题目】在△ABC中，内角A、B、C的对边分别为a、b、c，且
．
（1）求
的值；
（2）若cosB
，△ABC的面积为
，求△ABC的周长．
【答案】（1）2（2）5
【解析】
（1）利用正弦定理，两角和的正弦函数公式化简已知等式即可求解；
（2）由（1）利用正弦定理可得
，利用同角三角函数基本关系式可求
的值，结合三角形的面积公式可求
，联立解得
，
的值，根据余弦定理可求
的值，即可得解三角形的周长．
（1）∵
，
∴sinBcosA﹣2sinBcosC＝2sinCcosB﹣sinAcosB，sinBcosA+sinAcosB＝2sinCcosB+2sinBcosC，
可得sin（A+B）＝2sin（B+C），即sinC＝2sinA，
∴
2．
（2）∵由（1）可得sinC＝2sinA，
∴由正弦定理可得c＝2a，①
∵cosB
，△ABC的面积为
，
∴sinB
，由
acsinB
ac，解得ac＝2，②
∴由①②可得a＝1，c＝2，
∴由余弦定理可得b
2，
∴△ABC的周长a+b+c＝1+2+2＝5．
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABCA1B1C1中，AB AC，点E，F分别在棱BB1，CC1上（均异于端点），且∠ABE∠ACF，AE⊥BB1，AF⊥CC1．
求证：（1）平面AEF⊥平面BB1C1C；
（2）BC //平面AEF．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A﹣BCD，则在三棱锥A﹣BCD中，下列判断正确的是_____．（写出所有正确的序号）
①平面ABD⊥平面ABC
②直线BC与平面ABD所成角是45°
③平面ACD⊥平面ABC
④二面角C﹣AB﹣D余弦值为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，正方体
的棱长为2，
、
分别为棱
、
上的点，且与顶点不重合.
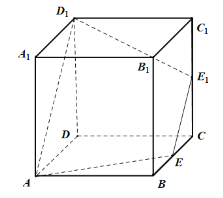
（1）若直线
与
相交于点
，求证：
、
、三点共线；
（2）若、分别为、的中点.
（ⅰ）求证：几何体
为棱台；
（ⅱ）求棱台的体积.
（附：棱台的体积公式
，其中
、
分别为棱台上下底面积，
为棱台的高）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥PABC中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.
（Ⅰ）证明MN∥平面PAB;
（Ⅱ）求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2020年是中国传统的农历“鼠年”，有人用3个圆构成“卡通鼠”的形象，如图：
是圆Q的圆心，圆Q过坐标原点O；点L、S均在x轴上，圆L与圆S的半径都等于2，圆S、圆L均与圆Q外切.已知直线l过点O.
（1）若直线l与圆L、圆S均相切，则l截圆Q所得弦长为__________；
（2）若直线l截圆L、圆S、圆Q所得弦长均等于d，则
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
