练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在中，D，E分别为AB，AC的中点，，以DE为折痕将折起，使点A到达点P的位置，如图.

    （1）证明：；

    （2）若平面DEP平面BCED，求直线DC与平面BCP所成角的正弦值。

    【答案】（1）见证明（2）

    【解析】

    （1）利用三角形的中位线得到，根据线面平行的判定定理证得；

    （2）利用面面垂直的性质，得到线线垂直，从而得到建立空间直角坐标系的条件，利用向量法求得线面所成角的正弦值.

    （1）（1）证明：D，E分别为AB，AC的中点，则，

    又，，则。

    （2）因为平面平面，平面平面，平面，.

    所以平面. 又因为平面，所以.

    以为坐标原点，分别以，，的方向为轴、轴、轴的正方向建立如图所示的空间直角坐标系

    在题图1中，设，则，，，.

    则，，，.

    所以，，.

    设为平面的法向量，

    则，即

    令，则.所以.

    设DC与平面BCP所成的角为，

    则.

    所以直线DC与平面BCP所成角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A﹣BCD，则在三棱锥A﹣BCD中，下列判断正确的是_____．（写出所有正确的序号）

    ①平面ABD⊥平面ABC

    ②直线BC与平面ABD所成角是45°

    ③平面ACD⊥平面ABC

    ④二面角C﹣AB﹣D余弦值为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年是中国传统的农历“鼠年”，有人用3个圆构成“卡通鼠”的形象，如图：是圆Q的圆心，圆Q过坐标原点O；点L、S均在x轴上，圆L与圆S的半径都等于2，圆S、圆L均与圆Q外切.已知直线l过点O.

    （1）若直线l与圆L、圆S均相切，则l截圆Q所得弦长为__________；

    （2）若直线l截圆L、圆S、圆Q所得弦长均等于d，则__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方形中， ， ，现将沿折起，使折到的位置且在面的射影恰好在线段上.

    （Ⅰ）证明： ；

    （Ⅱ）求锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

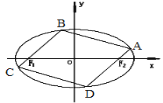
    【题目】已知椭圆C的方程为，为椭圆C的左右焦点，离心率为，短轴长为2。

    （1）求椭圆C的方程；

    （2）如图，椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点，求该平行四边形ABCD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(文)(2017·开封二模)为备战某次运动会，某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.

    (1)经过备战训练，从6人中随机选出2人进行成果检验，求选出的2人中至少有1个女运动员的概率．

    (2)检验结束后，甲、乙两名运动员的成绩用茎叶图表示如图：

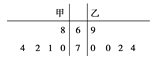
    计算说明哪位运动员的成绩更稳定．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的多面体中，四边形ABCD为菱形，，，面ABCD，，，异面直线AF，CD所成角的余弦值为．

    Ⅰ求证：面面EDB；

    Ⅱ求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l：x＋2y－2＝0.

    （1）求直线l1：y＝x－2关于直线l对称的直线l2的方程；

    （2）求直线l关于点A(1,1)对称的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线，.

    (1)直线是否过定点？若过定点，求出该定点坐标，若不过定点，请说明理由;

    (2)已知点，若直线上存在点满足条件，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案