
科目: 来源: 题型:
【题目】下边的折线图给出的是甲、乙两只股票在某年中每月的收盘价格,已知股票甲的极差是6.88元,标准差为2.04元;股票乙的极差为27.47元,标准差为9.63元,根据这两只股票在这一年中的波动程度,给出下列结论:①股票甲在这一年中波动相对较小,表现的更加稳定;②购买股票乙风险高但可能获得高回报;③股票甲的走势相对平稳,股票乙的股价波动较大;④两只般票在全年都处于上升趋势.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
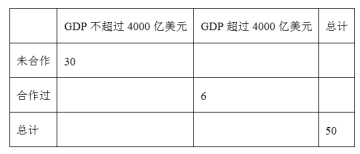
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4 坐标系与参数方程选讲
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 极坐标方程为
极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的参数方程;
的参数方程;
(2)当![]() 时,
时,![]() 为曲线
为曲线![]() 上动点,求点
上动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年11月,第2届中国国际进口博览会在中国上海召开,盛况空前,吸引了全球2800多家企业来参加.为评估企业的竞争力和长远合作能力,需要调查企业所在国家的经济状况.某机构抽取了50个国家,按照它们2017年的GDP总量,将收集的数据分成![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() (单位:亿美元)五组,做出下图的频率分布直方图:
(单位:亿美元)五组,做出下图的频率分布直方图:
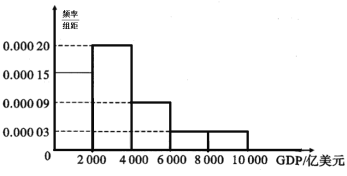
(1)试根据频率分布直方图估计这些国家的平均GDP(同一组中的数据用该组区间的中点值代表).
(2)研究人员发现所抽取的50个国家中,有些很早就与中国建交开展合作,有些近期才开始与中国合作,将两类国家分为“合作过”和“未合作过”.请根据频率分布直方图完成上表,并说明是否有95﹪的把握说明这些国家的GDP超过4000亿美元与中国合作有关.
查看答案和解析>>
科目: 来源: 题型:
【题目】某研究机构随机调查了![]() ,
,![]() 两个企业各100名员工,得到了
两个企业各100名员工,得到了![]() 企业员工月均收入的频数分布表以及
企业员工月均收入的频数分布表以及![]() 企业员工月均收入的统计图如下:
企业员工月均收入的统计图如下:
![]() 企业:
企业:
工资 | 人数 |
| 5 |
| 10 |
| 20 |
| 42 |
| 18 |
| 3 |
| 1 |
| 1 |
![]() 企业:
企业:
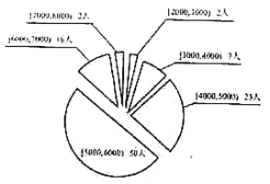
(1)若将频率视为概率,现从![]() 企业中随机抽取一名员工,求该员工月均收入不低于5000元的概率;
企业中随机抽取一名员工,求该员工月均收入不低于5000元的概率;
(2)(i)若从![]() 企业的月均收入在
企业的月均收入在![]() 员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,则2人月均收入都不在
员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,则2人月均收入都不在![]() 的概率是多少?
的概率是多少?
(ii)若你是一名即将就业的大学生,根据上述调查结果,并结合统计学相关知识,你会选择去哪个企业就业,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如上图.现在图(3)中随机选取一个点,则此点取自阴影部分的概率为________

查看答案和解析>>
科目: 来源: 题型:
【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是( )
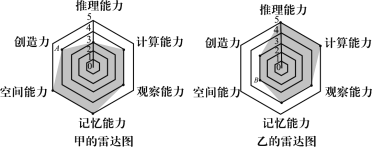
A.甲的六大能力中推理能力最差B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力D.乙的六大能力整体水平低于甲
查看答案和解析>>
科目: 来源: 题型:
【题目】
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:
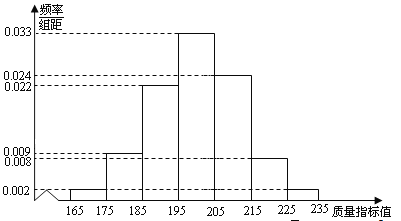
(I)求这500件产品质量指标值的样本平均值![]() 和样本方差
和样本方差![]() (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)某用户从该企业购买了100件这种产品,记![]() 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间![]() 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求![]() .
.
附:![]()
若![]() 则
则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com