
科目: 来源: 题型:
【题目】已知点A,B的坐标分别为(-2,0),(2,0).三角形ABM的两条边AM,BM所在直线的斜率之积是-![]() .
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)设直线AM方程为![]() ,直线l方程为x=2,直线AM交l于P,点P,Q关于x轴对称,直线MQ与x轴相交于点D.若△APD面积为2
,直线l方程为x=2,直线AM交l于P,点P,Q关于x轴对称,直线MQ与x轴相交于点D.若△APD面积为2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目: 来源: 题型:
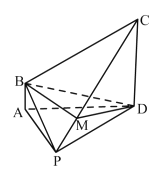
【题目】如图,在四棱锥PABCD-中,AB//CD,AB=1,CD=3,AP=2,DP=2![]() ,PAD=60°,AB⊥平面PAD,点M在棱PC上.
,PAD=60°,AB⊥平面PAD,点M在棱PC上.
(Ⅰ)求证:平面PAB⊥平面PCD;
(Ⅱ)若直线PA// 平面MBD,求此时直线BP与平面MBD所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】春节期间某商店出售某种海鲜礼盒,假设每天该礼盒的需求量在![]() 范围内等可能取值,该礼盒的进货量也在
范围内等可能取值,该礼盒的进货量也在![]() 范围内取值(每天进1次货).商店每销售1盒礼盒可获利50元;若供大于求,剩余的削价处理,每处理1盒礼盒亏损10元;若供不应求,可从其它商店调拨,销售1盒礼盒可获利30元.设该礼盒每天的需求量为
范围内取值(每天进1次货).商店每销售1盒礼盒可获利50元;若供大于求,剩余的削价处理,每处理1盒礼盒亏损10元;若供不应求,可从其它商店调拨,销售1盒礼盒可获利30元.设该礼盒每天的需求量为![]() 盒,进货量为
盒,进货量为![]() 盒,商店的日利润为
盒,商店的日利润为![]() 元.
元.
(1)求商店的日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)试计算进货量![]() 为多少时,商店日利润的期望值最大?并求出日利润期望值的最大值.
为多少时,商店日利润的期望值最大?并求出日利润期望值的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 、
、![]() 为抛物线
为抛物线![]() 上的两点,
上的两点,![]() 与
与![]() 的中点的纵坐标为4,直线
的中点的纵坐标为4,直线![]() 的斜率为
的斜率为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() 、
、![]() 为抛物线
为抛物线![]() (除原点外)上的不同两点,直线
(除原点外)上的不同两点,直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且满足
,且满足![]() ,记抛物线
,记抛物线![]() 在
在![]() 、
、![]() 处的切线交于点
处的切线交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com