【题目】如图，从参加环保知识竞赛的1200名学生中抽出名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：

（1）这一组的频数、频率分别是多少？

（2）估计这次环保知识竞赛的及格率。（分及以上为及格）

（3）若准备取成绩最好的300名发奖，则获奖的最低分数约为多少？

【题目】在直角坐标系中，直线与抛物线交于，两点，且.

（1）求的方程；

（2）试问：在轴的正半轴上是否存在一点，使得的外心在上？若存在，求的坐标；若不存在，请说明理由..

【题目】某运输公司有名驾驶员和名工人，有辆载重量为吨的甲型卡车和辆载重量为吨的乙型卡车.某天需运往地至少吨的货物，派用的车需满载且只运送一次.派用的每辆甲型卡车需配名工人，运送一次可得利润元：派用的每辆乙型卡车需配名工人，运送一次可得利润元，该公司合理计划当天派用两类卡车的车辆数，可得的最大利润多少？

【题目】已知偶函数满足，现给出下列命题：①函数是以2为周期的周期函数；②函数是以4为周期的周期函数；③函数为奇函数；④函数为偶函数，则其中真命题的个数是（ ）

A. 1 B. 2 C. 3 D. 4

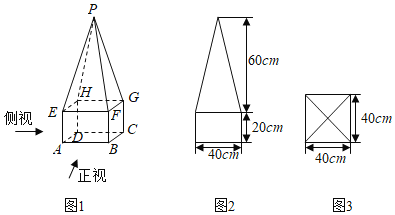
（1）请画出该安全标识墩的侧视图；

（2）求该安全标识墩的体积．

【题目】如图，直线与抛物线（常数）相交于不同的两点、，且（为定值），线段的中点为，与直线平行的切线的切点为（不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线，这个公共点为切点）．

（1）用、表示出点、点的坐标，并证明垂直于轴；

（2）求的面积，证明的面积与、无关，只与有关；

（3）小张所在的兴趣小组完成上面两个小题后，小张连、，再作与、平行的切线，切点分别为、，小张马上写出了、的面积，由此小张求出了直线与抛物线围成的面积，你认为小张能做到吗？请你说出理由．

现有抛物线:，直线：（其中，，是常数，且），直线交抛物线于，两点，设弦的阿氏三角形是.

（1）指出抛物线的焦点坐标和准线方程；

（2）求的面积（用，，表示）；

（3）称的阿氏为一阶的；、的阿氏、为二阶的；、、、的阿氏三角形为三阶的；……，由此进行下去，记所有的阶阿氏三角形的面积之和为，探索与之间的关系，并求.

【题目】现代城市大多是棋盘式布局（如北京道路几乎都是东西和南北走向）.在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离（位移），而是实际路程（如图）.在直角坐标平面内，我们定义，两点间的“直角距离”为：.

（1）在平面直角坐标系中，写出所有满足到原点的“直角距离”为2的“格点”的坐标.（格点指横、纵坐标均为整数的点）

（2）求到两定点、的“直角距离”和为定值的动点轨迹方程，并在直角坐标系内作出该动点的轨迹.（在以下三个条件中任选一个做答）

①，，；

②，，；

③，，.

（3）写出同时满足以下两个条件的“格点”的坐标，并说明理由（格点指横、纵坐标均为整数的点）.

①到，两点“直角距离”相等；

②到，两点“直角距离”和最小.

【题目】已两动圆和，把它们的公共点的轨迹记为曲线，若曲线与轴的正半轴交点为，且曲线上异于点的相异两点、满足.

(1)求曲线的方程；

(2)证明直线恒经过一定点，并求出此定点的坐标.

232 321 230 023 123 021 132 220 001

231 130 133 231 031 320 122 103 233

由此可以估计，恰好第三次就停止的概率为

A. B. C. D.