
科目: 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源租赁汽车”.每次租车收费的标准由两部分组成:①里程计费:1元/公里;②时间计费:![]() 元/分.已知陈先生的家离上班公司
元/分.已知陈先生的家离上班公司![]() 公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为
公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为![]() (分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示
(分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示

将各时间段发生的频率视为概率,一次路上开车所用的时间视为用车时间,范围为![]()
![]() 分.
分.
(1)估计陈先生一次租用新能源租赁汽车所用的时间不低于![]() 分钟的概率;
分钟的概率;
(2)若公司每月发放![]() 元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按
元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按![]() 天计算),并说明理由.(同一时段,用该区间的中点值作代表)
天计算),并说明理由.(同一时段,用该区间的中点值作代表)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直线坐标系中,定义![]() 为两点
为两点![]() 的“切比雪夫距离”,又设点P及
的“切比雪夫距离”,又设点P及![]() 上任意一点Q,称
上任意一点Q,称![]() 的最小值为点P到直线
的最小值为点P到直线![]() 的“切比雪夫距离”记作
的“切比雪夫距离”记作![]() 给出下列四个命题:( )
给出下列四个命题:( )
①对任意三点A、B、C,都有![]()
②已知点P(3,1)和直线![]() 则
则![]()
③到定点M的距离和到M的“切比雪夫距离”相等点的轨迹是正方形;
④定点![]() 动点
动点![]() 满足
满足![]() 则点P的轨迹与直线
则点P的轨迹与直线![]() (
(![]() 为常数)有且仅有2个公共点。
为常数)有且仅有2个公共点。
其中真命题的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若过点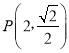 的直线l与椭圆C恒有公共点,求实数a的取值范围;
的直线l与椭圆C恒有公共点,求实数a的取值范围;
(2)若存在以点B(0,2)为圆心的圆与椭圆C有四个公共点,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,且AD∥BC,AD⊥CD,∠ABC=60°,BC=2AD=2,PC=3,△PAB是正三角形.
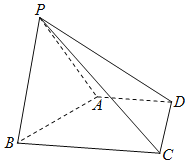
(1)求证:AB⊥PC;
(2)求二面角P﹣CD﹣B的平面角的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为F1,F2,离心率为
的左、右焦点为F1,F2,离心率为![]() ,且点
,且点![]() 在椭圆上.
在椭圆上.
(1)求椭圆C的标准方程;
(2)若直线l过点M(0,﹣2)且与椭圆C相交于A,B两点,且△OAB(O为坐标原点)的面积为![]() ,求出直线l的方程.
,求出直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
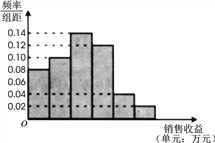
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com