
科目: 来源: 题型:
【题目】如图,已知四面体ABCD中,DA=DB=DC=![]() 且DA、DB、DC两两互相垂直,点
且DA、DB、DC两两互相垂直,点![]() 是△ABC的中心.
是△ABC的中心.

(1)求直线DA与平面ABC所成角的大小(用反三角函数表示);
(2)过![]() 作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
(3)将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与直线BC所成角记为![]() ,求
,求![]() 的取值范图.
的取值范图.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面直角坐标系内的动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离比为
的距离比为![]() .
.
(1)求动点P所在曲线E的方程;
(2)设点Q为曲线E与![]() 轴正半轴的交点,过坐标原点O作直线
轴正半轴的交点,过坐标原点O作直线![]() ,与曲线E相交于异于点
,与曲线E相交于异于点![]() 的不同两点
的不同两点![]() ,点C满足
,点C满足![]() ,直线
,直线![]() 和
和![]() 分别与以C为圆心,
分别与以C为圆心,![]() 为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比
为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
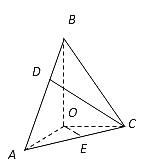
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
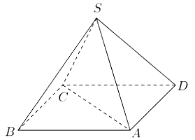
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 为空间中三条互相平行且两两间的距离分别为4、5、6的直线,给出下列三个结论:
为空间中三条互相平行且两两间的距离分别为4、5、6的直线,给出下列三个结论:
①存在![]() 使得
使得![]() 是直角三角形;
是直角三角形;
②存在![]() 使得
使得![]() 是等边三角形;
是等边三角形;
③三条直线上存在四点![]() 使得四面体
使得四面体![]() 为在一个顶点处的三条棱两两互相垂直的四面体,其中,所有正确结论的个数是( )
为在一个顶点处的三条棱两两互相垂直的四面体,其中,所有正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
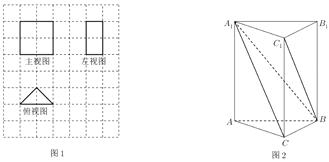
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
(2)在堑堵![]() 中,如图2,
中,如图2,![]() ,若
,若![]() ,当阳马
,当阳马![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】质检部门从某超市销售的甲、乙两种食用油中分别随机抽取100桶检测某项质量指标,由检测结果得到如图的频率分布直方图:
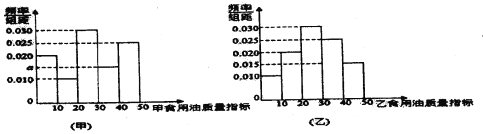
(I)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,试比较
,试比较![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)佑计在甲、乙两种食用油中各随机抽取1桶,恰有一个桶的质量指标大于20,且另—个桶的质量指标不大于20的概率;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得![]() :
:
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com