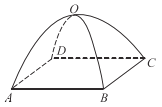
【题目】祖暅是我国南北朝时代的伟大科学家，在数学上有突出贡献，他在实践的基础上提出了体积计算原理（祖暅原理）：“幂势既同，则积不容异．”教材中的“探究与发现”利用祖暅原理将半球的体积转化为一个圆柱与一个圆锥的体积之差，从而得出球的体积计算公式．如图（1）是一种“四脚帐篷”的示意图，用任意平行于帐篷底面的平面截帐篷，得截面四边形为正方形，该帐篷的三视图如图（2）所示，其中正视图的投影线方向垂直于平面，正视图和侧视图中的曲线均为半径为1的半圆．模仿上述球的体积计算方法，得该帐篷的体积为（ ）．

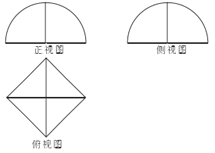
图（1） 图（2）

A.B.C.D.

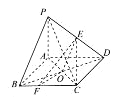
【题目】如图所示，底面为正方形的四棱锥P－ABCD中，AB=2，PA=4，PB=PD=，AC与BD相交于点O，E为PD中点．

(1)求证：EO//平面PBC；

(2)设线段BC上点F满足CF=2BF，求锐二面角E－OF－C的余弦值．

【题目】在平行四边形中，过点的直线与线段分别相交于点，若.

（1）求关于的函数解析式；

（2）定义函数，点列在函数的图像上，且数列是以1为首项，为公比的等比数列，为原点，令，是否存在点，使得？若存在，求出点的坐标，若不存在，说明理由.

（3）设函数为上的偶函数，当时，函数的图像关于直线对称，当方程在上有两个不同的实数解时，求实数的取值范围.

【题目】在直角坐标系中，曲线C的方程为．以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为．

(1)求曲线C的参数方程和直线的直角坐标方程；

(2)若直线与轴和y轴分别交于A，B两点，P为曲线C上的动点，求△PAB面积的最大值．

【题目】已知椭圆的短轴长为，且离心率为，圆．

(1)求椭圆C的方程，

(2)点P在圆D上，F为椭圆右焦点，线段PF与椭圆C相交于Q，若，求的取值范围．

【题目】已知点A,B,C,D是直角坐标系中不同的四点，若，，且，则下列说法正确的是( ),

A.C可能是线段AB的中点

B.D可能是线段AB的中点

C.C、D可能同时在线段AB上

D.C、D不可能同时在线段AB的延长线上

【题目】已知函数．

(1)求函数的单调区间及极值；

(2)设时，存在，使方程成立，求实数的最小值．

A. B. C. D.

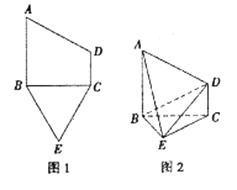
(1)求证:平面ABE丄平面ADE；

(2)若AB=BC,求二面角A-DE-B的余弦值.

【题目】已知直线，，过点的直线分别与直线，交于，其中点在第三象限，点在第二象限，点；

（1）若的面积为，求直线的方程；

（2）直线交于点，直线交于点，若直线的斜率均存在，分别设为，判断是否为定值？若为定值，求出该定值；若不为定值，说明理由．