【题目】如图1，在边长为3的菱形中，已知，且.将梯形沿直线折起，使平面，如图2，分别是上的点.

（1）求证：图2中，平面平面；

（2）若平面平面，求三棱锥的体积.

男：164 178 174 185 170 158 163 165 161 170

女：165 168 156 170 163 162 158 153 169 172

（1）根据测量结果完成身高的茎叶图（单位：厘米），并分别求出男、女生身高的平均值.

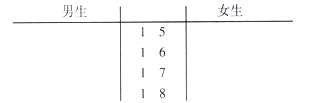
（2）请根据测量结果得到20名学生身高的中位数（单位：厘米），将男、女生身高不低于和低于的人数填入下表中，并判断是否有的把握认为男、女生身高有差异？

参照公式：

（3）若男生身高低于165厘米为偏矮，不低于165厘米且低于175厘米为正常，不低于175厘米为偏高.假设可以用测量结果的频率代替概率，试求从高二的男生中任意选出2人，恰有1人身高属于正常的概率.

【题目】如图1，在边长为3的菱形中，已知，且.将梯形沿直线折起，使平面，如图2，分别是上的点.

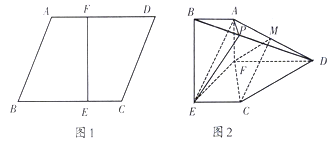
（1）求证：图2中，平面平面；

（2）若平面平面，求三棱锥的体积.

【题目】已知函数，.

（1）若，求实数取值的集合；

（2）证明：

【题目】在平面直角坐标系中，已知圆经过，，三点，是线段上的动点，，是过点且互相垂直的两条直线，其中交轴于点，交圆于、两点．

（1）若，求直线的方程；

（2）若是使恒成立的最小正整数.

①求的值；

②求三角形的面积的最小值．

【题目】如图所示，在四棱锥中，底面是边长为1的菱形，，面，，、分别为、的中点.

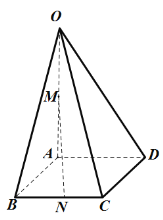
（1）证明：直线平面；

（2）求异面直线与所成角的大小；

（3）求点到平面的距离．

【题目】已知椭圆的短轴长为，离心率为。

（1）求椭圆的标准方程;

（2）设椭圆的左，右焦点分别为，左，右顶点分别为，，点，，为椭圆上位于轴上方的两点，且，记直线，的斜率分别为，，若，求直线的方程.

【题目】六棱锥中，底面是正六边形，底面，给出下列四个命题：

①线段的长是点到线段的距离；

②异面直线与所成角是；

③线段的长是直线与平面的距离；

④是二面角平面角.

其中所有真命题的序号是_______________.

【题目】设，是两条不同的直线，，，是三个不同的平面．有下列四个命题：

①若，，，则；

②若，，则；

③若，，，则；

④若，，，则．

其中正确命题的序号是（ ）

A.①③B.①④C.②③④D.②③

【题目】如图①，在等腰梯形中，，，分别为，的中点，，为中点现将四边形沿折起,使平面平面，得到如图②所示的多面体在图②中，

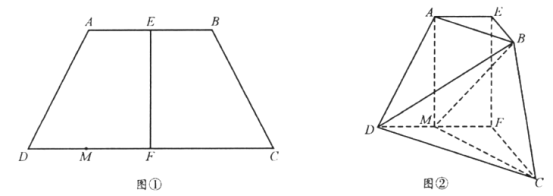
（1）证明：；

（2）求二面角的余弦值。