
科目: 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)经过点(
1(a>b>0)经过点(![]() ,1),F(0,1)是C的一个焦点,过F点的动直线l交椭圆于A,B两点.
,1),F(0,1)是C的一个焦点,过F点的动直线l交椭圆于A,B两点.
(1)求椭圆C的方程
(2)是否存在定点M(异于点F),对任意的动直线l都有kMA+kMB=0,若存在求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.
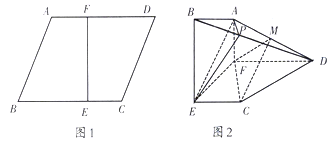
(1)若平面![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(2)是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,马路![]() 南边有一小池塘,池塘岸
南边有一小池塘,池塘岸![]() 长40米,池塘的最远端
长40米,池塘的最远端![]() 到
到![]() 的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路
的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路![]() ,且
,且![]() 均与小池塘岸线相切,记
均与小池塘岸线相切,记![]() .
.

(1)求小路的总长,用![]() 表示;
表示;
(2)若在小路与小池塘之间(图中阴影区域)铺上草坪,求所需铺草坪面积最小时,![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为研究男、女生的身高差异,现随机从高二某班选出男生、女生各10人,并测量他们的身高,测量结果如下(单位:厘米):
男:164 178 174 185 170 158 163 165 161 170
女:165 168 156 170 163 162 158 153 169 172
(1)根据测量结果完成身高的茎叶图(单位:厘米),并分别求出男、女生身高的平均值.

(2)请根据测量结果得到20名学生身高的中位数![]() (单位:厘米),将男、女生身高不低于
(单位:厘米),将男、女生身高不低于![]() 和低于
和低于![]() 的人数填入下表中,并判断是否有
的人数填入下表中,并判断是否有![]() 的把握认为男、女生身高有差异?
的把握认为男、女生身高有差异?
人数 | 男生 | 女生 |
身高 | ||
身高 |
参照公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
(3)若男生身高低于165厘米为偏矮,不低于165厘米且低于175厘米为正常,不低于175厘米为偏高.假设可以用测量结果的频率代替概率,试求从高二的男生中任意选出2人,恰有1人身高属于正常的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)若![]() ,求直线
,求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知F1,F2分别是椭圆C:![]() 1(>b>0)的左、右焦点,过F2且不与x轴垂直的动直线l与椭圆交于M,N两点,点P是椭圆C右准线上一点,连结PM,PN,当点P为右准线与x轴交点时有2PF2=F1F2.
1(>b>0)的左、右焦点,过F2且不与x轴垂直的动直线l与椭圆交于M,N两点,点P是椭圆C右准线上一点,连结PM,PN,当点P为右准线与x轴交点时有2PF2=F1F2.
(1)求椭圆C的离心率;
(2)当点P的坐标为(2,1)时,求直线PM与直线PN的斜率之和.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的左焦点为F(﹣1,0),离心率为
的左焦点为F(﹣1,0),离心率为![]() ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点F不与坐标轴垂直的直线交椭圆C于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列有关命题的说法正确的是__________________.
①命题“若x2-3x+2=0,则x=1”的逆否命题为:若x≠1,则x2-3x+2≠0
②x=1是x2-3x+2=0的充分不必要条件
③若p∧q为假命题,则p,q均为假命题
④对于命题p:x∈R,使得x2+x+1<0,则非p:x∈R, 均有x2+x+1≥0
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司推出一新款手机,因其功能强大,外观新潮,一上市便受到消费者争相抢购,销量呈上升趋势.散点图是该款手机上市后前6周的销售数据.
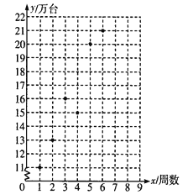
(1)根据散点图,用最小二乘法求![]() 关于
关于![]() 的线性回归方程,并预测该款手机第8周的销量;
的线性回归方程,并预测该款手机第8周的销量;
(2)为了分析市场趋势,该公司市场部从前6周的销售数据中随机抽取2周的数据,记抽取的销量在18万台以上的周数为![]() ,求
,求![]() 的分布列和数学期望.参考公式:回归直线方程
的分布列和数学期望.参考公式:回归直线方程![]() ,其中:
,其中: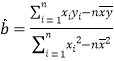 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com