
科目: 来源: 题型:
【题目】某小学为了解四年级学生的家庭作业用时情况,从本校四年级随机抽取了一批学生进行调查,并绘制了学生作业用时的频率分布直方图,如图所示.
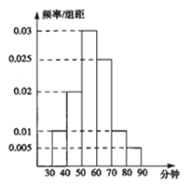
(1)估算这批学生的作业平均用时情况;
(2)作业用时不能完全反映学生学业负担情况,这与学生自身的学习习惯有很大关系如果用时四十分钟之内评价为优异,一个小时以上为一般,其它评价为良好.现从优异和良好的学生里面用分层抽样的方法抽取300人,其中女生有90人(优异20人).请完成列联表,并根据列联表分析能否在犯错误的概率不超过0.05的前提下认为学习习惯与性别有关系?
男生 | 女生 | 合计 | |
良好 | |||
优异 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为![]() ,且
,且![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)过点![]() 作互相垂直的两条直线,分别交曲线
作互相垂直的两条直线,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() ,若四边形
,若四边形![]() 面积为
面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]()
![]() 分别是双曲线
分别是双曲线![]()
![]() 的左、右焦点,A为左顶点,P为双曲线右支上一点,若
的左、右焦点,A为左顶点,P为双曲线右支上一点,若![]() 且
且![]() 的最小内角为
的最小内角为![]() ,则( )
,则( )
A.双曲线的离心率![]() B.双曲线的渐近线方程为
B.双曲线的渐近线方程为![]()
C.![]() D.直线
D.直线![]() 与双曲线有两个公共点
与双曲线有两个公共点
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,且
的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,且![]() ,M为AB中点,则下列结论正确的是( )
,M为AB中点,则下列结论正确的是( )
A.![]() B.
B.![]() 为等腰直角三角形
为等腰直角三角形
C.直线AB的斜率为![]() D.
D.![]() 的面积为4
的面积为4
查看答案和解析>>
科目: 来源: 题型:
【题目】某大城市一家餐饮企业为了了解外卖情况,统计了某个送外卖小哥某天从9:00到21:00这个时间段送的50单外卖.以2小时为一时间段将时间分成六段,各时间段内外卖小哥平均每单的收入情况如下表,各时间段内送外卖的单数的频率分布直方图如下图.
时间区间 |
|
|
|
|
|
|
每单收入(元) | 6 | 5.5 | 6 | 6.4 | 5.5 | 6.5 |
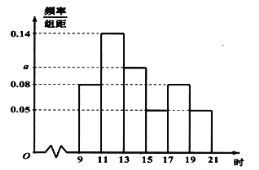
(Ⅰ)求频率分布直方图中![]() 的值,并求这个外卖小哥送这50单获得的收入;
的值,并求这个外卖小哥送这50单获得的收入;
(Ⅱ)在这个外卖小哥送出的50单外卖中男性订了25单,且男性订的外卖中有20单带饮品,女性订的外卖中有10单带饮品,请完成下面的![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“带饮品和男女性别有关”?
的把握认为“带饮品和男女性别有关”?
带饮品 | 不带饮品 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]()
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (t为参数).直线
(t为参数).直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com