
科目: 来源: 题型:
【题目】短道速滑队组织6名队员(包括赛前系列赛积分最靠前的甲乙丙三名队员在内)参加冬奥会选拔赛,记“甲得第一名”为![]() ,“乙得第二名”为
,“乙得第二名”为![]() ,“丙得第三名”为
,“丙得第三名”为![]() ,若
,若![]() 是真命题,
是真命题,![]() 是假命题,
是假命题,![]() 是真命题,则选拔赛的结果为( )
是真命题,则选拔赛的结果为( )
A.甲得第一名、乙得第三名、丙得第二名
B.甲没得第一名、乙没得第二名、丙得第三名
C.甲得第一名、乙没得第二名、丙得第三名
D.甲得第二名、乙得第一名、丙得第三名
查看答案和解析>>
科目: 来源: 题型:
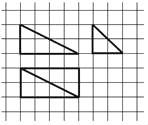
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 、
、![]() 满足
满足![]()
![]()
![]() ,其中
,其中![]() 数列
数列![]() 的前
的前![]() 项和,
项和,
(1)若数列![]() 是首项为
是首项为![]() .公比为
.公比为![]() 的等比数列,求数列
的等比数列,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() 求证:数列
求证:数列![]() 满足
满足![]()
![]()
![]() ,并写出
,并写出![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设![]() ,求证
,求证![]() 中任意一项总可以表示成该数列其它两项之积.
中任意一项总可以表示成该数列其它两项之积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
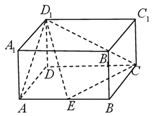
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是由菱形![]() ,平行四边形
,平行四边形![]() 和矩形
和矩形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,将其沿
,将其沿![]() ,
,![]() 折起使得
折起使得![]() 与
与![]() 重合,如图2.
重合,如图2.

(1)证明:图2中的平面![]() 平面
平面![]() ;
;
(2)求图2中点![]() 到平面
到平面![]() 的距离;
的距离;
(3)求图2中二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=ax+![]() (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
程为y=3.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,
并求出此定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]()
![]() 过点
过点![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 、
、![]() 为椭圆的左、右焦点,直线
为椭圆的左、右焦点,直线![]() 过
过![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,求△
两点,求△![]() 面积的最大值;
面积的最大值;
(3)求动点![]() 的轨迹方程,使得过点
的轨迹方程,使得过点![]() 存在两条互相垂直的直线
存在两条互相垂直的直线![]() 、
、![]() ,且都与椭圆只有一个公共点.
,且都与椭圆只有一个公共点.
查看答案和解析>>
科目: 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量.2007年至2018年,某企业连续12年累计研发投入达4100亿元,我们将研发投入与经营收入的比值记为研发投入占营收比.这12年间的研发投入(单位:十亿元)用图中的条形图表示,研发投入占营收比用图中的折线图表示.
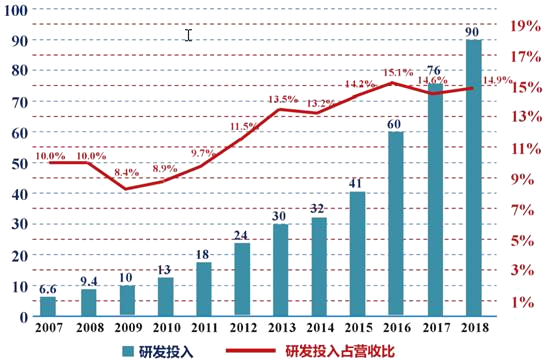
根据折线图和条形图,下列结论错误的是( )
A. 2012﹣2013 年研发投入占营收比增量相比 2017﹣2018 年增量大
B. 该企业连续 12 年研发投入逐年增加
C. 2015﹣2016 年研发投入增值最大
D. 该企业连续 12 年研发投入占营收比逐年增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com