
科目: 来源: 题型:
【题目】如图,长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别在
分别在![]() 上,
上,![]()
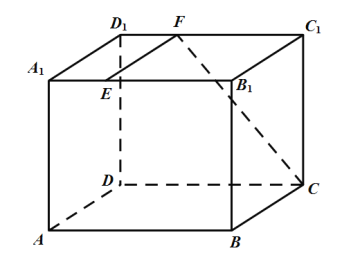
(1)求直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)过点![]() 的平面
的平面![]() 与此长方体的表面相交,交线围成一个正方形,求平面
与此长方体的表面相交,交线围成一个正方形,求平面![]() 把该长方体分成的两部分体积的比值.
把该长方体分成的两部分体积的比值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形, ![]() .
.

(Ⅰ)若![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 与平面
与平面![]() 所成角.
所成角.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校进入高中数学竞赛复赛的学生中,高一年级有6人,高二年级有12人, 高三年级有24人,现采用分层抽样的方法从这些学生中抽取7人进行采访.
(1)求应从各年级分别抽取的人数;
(2)若从抽取的7人中再随机抽取2人做进一步了解(注高一学生记为![]() ,高二学生记为
,高二学生记为![]() ,高三学生记为
,高三学生记为![]() ,
,![]() )
)
①列出所有可能的抽取结果;
②求抽取的2人均为高三年级学生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,椭圆![]() 离心率为
离心率为![]() ,
,![]() 、
、![]() 是椭圆C的短轴端点,且
是椭圆C的短轴端点,且![]() 到焦点的距离为
到焦点的距离为![]() ,点M在椭圆C上运动,且点M不与
,点M在椭圆C上运动,且点M不与![]() 、
、![]() 重合,点N满足
重合,点N满足![]() .
.
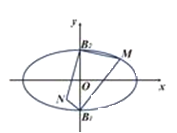
(1)求椭圆C的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
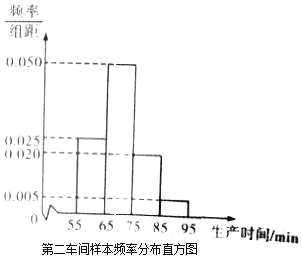
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中随机抽取2人,求抽取的2人中,至少1人生产时间小于65min的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在等差数列![]() 中,
中,![]() ,
,![]() .令
.令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)是否存在正整数![]() ,(
,(![]()
![]() ),使得
),使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的![]() ,
,![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】无穷等差数列![]() 的各项均为整数,首项为
的各项均为整数,首项为![]() 、公差为
、公差为![]() ,
,![]() 是其前
是其前![]() 项和,
项和,![]() 是其中的三项,给出下列命题:
是其中的三项,给出下列命题:
①对任意满足条件的![]() ,存在
,存在![]() ,使得
,使得![]() 一定是数列
一定是数列![]() 中的一项;
中的一项;
②存在满足条件的数列![]() ,使得对任意的
,使得对任意的![]() ,
,![]() 成立;
成立;
③对任意满足条件的![]() ,存在
,存在![]() ,使得
,使得![]() 一定是数列
一定是数列![]() 中的一项。
中的一项。
其中正确命题的序号为( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com