
科目: 来源: 题型:
【题目】某高校在2019年的冬令营考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| 35 | 0.350 |
第3组 |
| 10 | 0.100 |
第4组 |
| 20 | 0.200 |
第5组 |
| 30 | 0.300 |
合计 | 100 | 1.00 | |
(1)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,高校决定在这6名学生中,随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被A考官测试的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点
是参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 取最大值时
取最大值时![]() 的值
的值
查看答案和解析>>
科目: 来源: 题型:
【题目】黄金分割比例![]() 具有严格的比例性,艺术性,和谐性,蕴含着丰富的美学价值.这一比值能够引起人们的美感,被称为是建筑和艺术中最理想的比例.我们把离心率
具有严格的比例性,艺术性,和谐性,蕴含着丰富的美学价值.这一比值能够引起人们的美感,被称为是建筑和艺术中最理想的比例.我们把离心率![]() 的椭圆称为“黄金椭圆”,则以下四种说法中正确的个数为( )
的椭圆称为“黄金椭圆”,则以下四种说法中正确的个数为( )
①椭圆![]() 是“黄金椭圆;
是“黄金椭圆;
②若椭圆![]() ,
,![]() 的右焦点
的右焦点![]() 且满足
且满足![]() ,则该椭圆为“黄金椭圆”;
,则该椭圆为“黄金椭圆”;
③设椭圆![]() ,
,![]() 的左焦点为F,上顶点为B,右顶点为A,若
的左焦点为F,上顶点为B,右顶点为A,若![]() ,则该椭圆为“黄金椭圆”;
,则该椭圆为“黄金椭圆”;
④设椭圆,![]() ,
,![]() 的左右顶点分别A,B,左右焦点分别是
的左右顶点分别A,B,左右焦点分别是![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,则该椭圆为“黄金椭圆”;
成等比数列,则该椭圆为“黄金椭圆”;
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 为正三角形,
为正三角形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上一点(不与
上一点(不与![]() 、
、![]() 重合),平面
重合),平面![]() 交棱
交棱![]() 于点
于点![]() .
.
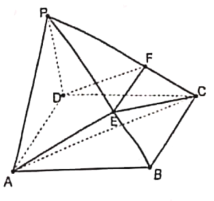
(1)求证:![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其中一个焦点为圆
,其中一个焦点为圆![]() 的圆心,右顶点是圆
的圆心,右顶点是圆![]() 与
与![]() 轴的一个交点.已知椭圆
轴的一个交点.已知椭圆![]() 与直线
与直线![]() 相交于
相交于![]() 、
、![]() 两点,延长
两点,延长![]() 与椭圆
与椭圆![]() 交于点
交于点![]() .
.
(1)求椭圆的方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=ax+![]() (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
程为y=3.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,
并求出此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com