【题目】如图，在四棱锥中， ， ∥，且 , ， .

（Ⅰ）求证：平面⊥平面；

（Ⅱ）求直线与平面所成角的正弦值．

（Ⅰ）求a的值；

（Ⅱ）设直线x=t（t＞0）分别与曲线y=f（x）和y=g（x）交于P，Q两点，求证：|PQ|＞2．

【题目】如图，已知位于轴左侧的圆与轴相切于点且被轴分成的两段圆弧长之比为，直线与圆相交于，两点，且以为直径的圆恰好经过坐标原点.

（1）求圆的方程；

（2）求直线的斜率的取值范围.

【题目】如图所示，在四棱锥中，底面是且边长为的菱形，侧面为正三角形，其所在平面垂直于底面，若为的中点，为的中点.

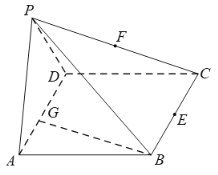
（1）求证：平面；

（2）求证：；

（3）在棱上是否存在一点，使平面平面，若存在，确定点的位置；若不存在，说明理由

【题目】已知椭圆的离心率为，M是椭圆C的上顶点，，F2是椭圆C的焦点，的周长是6．

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）过动点P（1，t）作直线交椭圆C于A，B两点，且|PA|=|PB|，过P作直线l，使l与直线AB垂直，证明：直线l恒过定点，并求此定点的坐标．

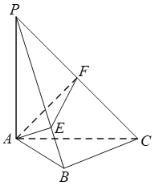
【题目】在《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑.如图，在鳖臑中，平面，，且，过点分别作于点，于点，连结，当的面积最大时，__________.

【题目】如图，中，，，若以，为焦点的双曲线的渐近线经过点，则该双曲线的离心率为

A. B.

C. D.

【题目】某绿色有机水果店中一款有机草莓味道鲜甜，店家每天以每斤元的价格从农场购进适量草莓，然后以每斤元的价格出售，如果当天卖不完，剩下的草莓由果汁厂以每斤元的价格回收.

（1）若水果店一天购进斤草莓，求当天的利润（单位：元）关于当天需求量（单位：斤，）的函数解析式；

（2）水果店记录了天草莓的日需求量（单位：斤），整理得下表：

①假设水果店在这天内每天购进斤草莓，求这天的日利润（单位：元）的平均数；

②若水果店一天购进斤草莓，以天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于元的概率.

【题目】已知，是异面直线，是，外的一点，则下列结论中正确的是（ ）

A.过有且只有一条直线与，都垂直B.过有且只有一条直线与，都平行

C.过有且只有一个平面与，都垂直D.过有且只有一个平面与，都平行

【题目】设数列的前n项和为,对一切,点都在函数的图像上.

（1）证明：当时,;

（2）求数列的通项公式;

（3）设为数列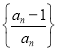的前n项的积,若不等式对一切成立,求实数a的取值范围.