【题目】已知某种细菌的适宜生长温度为10℃～25℃，为了研究该种细菌的繁殖数量（单位：个）随温度（单位：℃）变化的规律，收集数据如下：

对数据进行初步处理后，得到了一些统计量的值，如下表所示：

其中，.

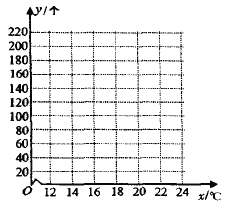
（1）请绘出关于的散点图，并根据散点图判断与哪一个更适合作为该种细菌的繁殖数量关于温度的回归方程类型（给出判断即可，不必说明理由）；

（2）根据（1）的判断结果及表格数据，建立关于的回归方程（结果精确到0.1）；

（3）当温度为25℃时，该种细菌的繁殖数量的预报值为多少？

参考公式：对于一组数据，其回归直线的斜率和截距的最小二成估计分别为，.

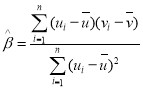参考数据：.

如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.

（1）证明：BE⊥平面EB1C1；

（2）若AE=A1E，求二面角B–EC–C1的正弦值.

【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，即杨辉三角，这是数学史上的一个伟大成就，在“杨辉三角”中，第行的所有数字之和为，若去除所有为1的项，依次构成数列2，3，3，4，6，4，5，10，10，5，…，则此数列的前15项和为（ ）

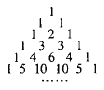
A. 110B. 114C. 124D. 125

【题目】在平面直角坐标系中，曲线过点，其参数方程为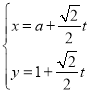（为参数，）.以为极点，轴非负半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）求曲线的普通方程和曲线的直角坐标方程；

（2）已知曲线与曲线交于两点，且，求实数的值.

（1）求该设备给企业带来的总利润（万元）与使用年数的函数关系；

（2）试计算这套设备使用多少年，可使年平均利润最大？年平均利润最大为多少万元？

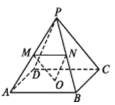
【题目】如图,在棱长均相等的四棱锥中, 为底面正方形的中心, ,分别为侧棱,的中点,有下列结论正确的有：( )

A.∥平面B.平面∥平面

C.直线与直线所成角的大小为D.

（1）根据频率分布直方图计算该种蔬果日需求量的平均数（同一组中的数据用该组区间中点值代表）；

（2）该经销商某天购进了250公斤这种蔬果，假设当天的需求量为公斤，利润为元.求关于的函数关系式，并结合频率分布直方图估计利润不小于1750元的概率.

【题目】如图，底面为矩形的四棱锥中，底面ABCD，，MN分别为ADPC中点.

(1)证明:平面PAB；

(2)求异面直线MN与AB所成角的大小.

【题目】如图所示，和所在平面互相垂直，且，，，分别为，的中点.

（1）求证：；

（2）求二面角的正弦值.

【题目】已知某种细菌的适宜生长温度为10℃～25℃，为了研究该种细菌的繁殖数量（单位：个）随温度（单位：℃）变化的规律，收集数据如下：

对数据进行初步处理后，得到了一些统计量的值，如下表所示：

其中，.

（1）请绘出关于的散点图，并根据散点图判断与哪一个更适合作为该种细菌的繁殖数量关于温度的回归方程类型（给出判断即可，不必说明理由）；

（2）根据（1）的判断结果及表格数据，建立关于的回归方程（结果精确到0.1）；

（3）当温度为25℃时，该种细菌的繁殖数量的预报值为多少？

参考公式：对于一组数据，其回归直线的斜率和截距的最小二成估计分别为，.

参考数据：.