（1）求B；

（2）求y=sinA-sinC的取值范围．

【题目】在平面直角坐标系中，定义为两点AB的“切比雪夫距离”，又设点P及上任意一点Q,称的最小值为点P到直线的“切比雪夫距离”，记作,给出下列三个命题：

①对任意三点A、B、C，都有

②已知点P(2,1)和直线,则

③定点动点P满足则点P的轨迹与直线(为常数)有且仅有2个公共点.

其中真命题的个数是（ ）

A.0B.1C.2D.3

【题目】在全国第五个“扶贫日”到来之前，某省开展“精准扶贫，携手同行”的主题活动，某贫困县调查基层干部走访贫困户数量．甲镇有基层干部60人，乙镇有基层干部60人，丙镇有基层干部80人，每人都走访了若干贫困户，按照分层抽样，从甲、乙、丙三镇共选20名基层干部，统计他们走访贫困户的数量，并将走访数量分成，，，，5组，绘制成如图所示的频率分布直方图．

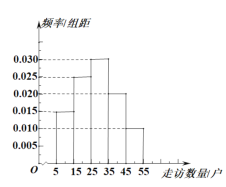
（1）求这20人中有多少人来自丙镇，并估计甲、乙、丙三镇的基层干部走访贫困户户数的中位数（精确到整数位）；

（2）如果把走访贫困户达到或超过35户视为工作出色，求选出的20名基层干部中工作出色的人数，并从中选2人做交流发言，求这2人中至少有一人走访的贫困户在的概率．

【题目】已知直线与抛物线：交于，两点，且的面积为16（为坐标原点）.

（1）求的方程.

（2）直线经过的焦点且不与轴垂直，与交于，两点，若线段的垂直平分线与轴交于点，试问在轴上是否存在点，使为定值？若存在，求该定值及的坐标；若不存在，请说明理由.

【题目】在全国第五个“扶贫日”到来之前，某省开展“精准扶贫，携手同行”的主题活动，某贫困县调查基层干部走访贫困户数量．甲镇有基层干部60人，乙镇有基层干部60人，丙镇有基层干部80人，每人都走访了若干贫困户，按照分层抽样，从甲、乙、丙三镇共选20名基层干部，统计他们走访贫困户的数量，并将走访数量分成，，，，5组，绘制成如图所示的频率分布直方图．

（1）求这20人中有多少人来自丙镇，并估计甲、乙、丙三镇的基层干部走访贫困户户数的中位数（精确到整数位）；

（2）如果把走访贫困户达到或超过35户视为工作出色，求选出的20名基层干部中工作出色的人数，并从中选2人做交流发言，求这2人中至少有一人走访的贫困户在的概率．

【题目】过抛物线的焦点且斜率为的直线交抛物线于，两点，且．

（1）求的值；

（2）抛物线上一点，直线（其中）与抛物线交于，两个不同的点（均与点不重合），设直线，的斜率分别为，，．动点在直线上，且满足，其中为坐标原点．当线段最长时，求直线的方程．

【题目】“伟大的变革—庆祝改革开放周年大型展览”于年月日在中国国家博物馆闭幕，本次特展紧扣“改革开放年光辉历程”的主线，多角度、全景式描绘了我国改革开放年波澜壮阔的历史画卷．据统计，展览全程呈现出持续火爆的状态，现场观众累计达万人次，参展人数屡次创造国家博物馆参观纪录，网上展馆点击浏览总量达亿次．

下表是年月参观人数（单位：万人）统计表

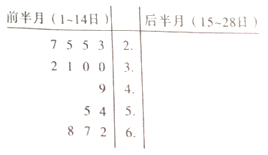
根据表中数据回答下列问题：

（1）请将年月前半月（日）和后半月（日）参观人数统计对比茎叶图填补完整，并通过茎叶图比较两组数据方差的大小（不要求计算出具体值，得出结论即可）；

（2）将年月参观人数数据用该天的对应日期作为样本编号，现从中抽样天的样本数据．若抽取的样本编号是以为公差的等差数列，且数列的第项为，求抽出的这个样本数据的平均值；

（3）根据国博以往展览数据及调查统计信息可知，单日入馆参观人数为（含，单位：万人）时，参观者的体验满意度最佳，在从中抽出的样本数据中随机抽取三天的数据，参观者的体验满意度为最佳的天数记为，求的分布列与期望．

【题目】在极坐标系中，曲线的方程为，以极点为原点，极轴所在直线为轴建立直角坐标，直线的参数方程为（为参数），与交于，两点．

（1）写出曲线的直角坐标方程和直线的普通方程；

（2）设点；若、、成等比数列，求的值

【题目】如图，已知点F为抛物线C：（）的焦点，过点F的动直线l与抛物线C交于M，N两点，且当直线l的倾斜角为45°时，.

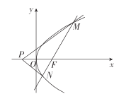
（1）求抛物线C的方程.

（2）试确定在x轴上是否存在点P，使得直线PM，PN关于x轴对称？若存在，求出点P的坐标；若不存在，请说明理由.