
科目: 来源: 题型:
【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: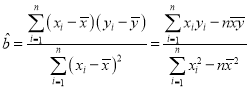 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在长方体![]() 中,点E是棱
中,点E是棱![]() 上的一个动点,若平面
上的一个动点,若平面![]() 交棱
交棱![]() 于点F,给出下列命题:
于点F,给出下列命题:
①四棱锥![]() 的体积恒为定值;
的体积恒为定值;
②对于棱![]() 上任意一点E,在棱
上任意一点E,在棱![]() 上均有相应的点G,使得
上均有相应的点G,使得![]() 平面
平面![]() ;
;
③O为底面![]() 对角线
对角线![]() 和
和![]() 的交点,在棱
的交点,在棱![]() 上存在点H,使
上存在点H,使![]() 平面
平面![]() ;
;
④存在唯一的点E,使得截面四边形![]() 的周长取得最小值.
的周长取得最小值.
其中为真命题的是____________________.(填写所有正确答案的序号)

查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,其中
,其中![]() ,点
,点![]() 是椭圆
是椭圆![]() 的右顶点,射线
的右顶点,射线![]() :
:![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)设椭圆![]() 的长半轴、短半轴的长分别为
的长半轴、短半轴的长分别为![]() 、
、![]() ,当
,当![]() 的值在区间
的值在区间 中变化时,求
中变化时,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,以![]() 为焦点,
为焦点,![]() 为顶点且开口方向向左的抛物线过点
为顶点且开口方向向左的抛物线过点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某海面上有![]() 、
、![]() 、
、![]() 三个小岛(面积大小忽略不计),
三个小岛(面积大小忽略不计),![]() 岛在
岛在![]() 岛的北偏东
岛的北偏东![]() 方向距
方向距![]() 岛
岛![]() 千米处,
千米处,![]() 岛在
岛在![]() 岛的正东方向距
岛的正东方向距![]() 岛20千米处.以
岛20千米处.以![]() 为坐标原点,
为坐标原点,![]() 的正东方向为
的正东方向为![]() 轴的正方向,1千米为单位长度,建立平面直角坐标系.圆
轴的正方向,1千米为单位长度,建立平面直角坐标系.圆![]() 经过
经过![]() 、
、![]() 、
、![]() 三点.
三点.

(1)求圆![]() 的方程;
的方程;
(2)若圆![]() 区域内有未知暗礁,现有一船D在
区域内有未知暗礁,现有一船D在![]() 岛的南偏西30°方向距
岛的南偏西30°方向距![]() 岛40千米处,正沿着北偏东
岛40千米处,正沿着北偏东![]() 行驶,若不改变方向,试问该船有没有触礁的危险?
行驶,若不改变方向,试问该船有没有触礁的危险?
查看答案和解析>>
科目: 来源: 题型:
【题目】
对于各项均为整数的数列![]() ,如果
,如果![]() (
(![]() =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数
列![]() 具有“
具有“![]() 性质”.
性质”.
不论数列![]() 是否具有“
是否具有“![]() 性质”,如果存在与
性质”,如果存在与![]() 不是同一数列的
不是同一数列的![]() ,且
,且![]() 同
同
时满足下面两个条件:①![]() 是
是![]() 的一个排列;②数列
的一个排列;②数列![]() 具有“
具有“![]() 性质”,则称数列
性质”,则称数列![]() 具有“变换
具有“变换![]() 性质”.
性质”.
(I)设数列![]() 的前
的前![]() 项和
项和![]() ,证明数列
,证明数列![]() 具有“
具有“![]() 性质”;
性质”;
(II)试判断数列1,2,3,4,5和数列1,2,3,…,11是否具有“变换![]() 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列![]() ,不具此性质的说明理由;
,不具此性质的说明理由;
(III)对于有限项数列![]() :1,2,3,…,
:1,2,3,…,![]() ,某人已经验证当
,某人已经验证当![]() 时,
时,
数列![]() 具有“变换
具有“变换![]() 性质”,试证明:当”
性质”,试证明:当”![]() 时,数列
时,数列![]() 也具有“变换
也具有“变换![]() 性质”.
性质”.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸x(mm)之间近似满足关系式
与尺寸x(mm)之间近似满足关系式![]() (b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
(b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸x(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量y (g) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(Ⅰ)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(ⅰ)根据所给统计量,求y关于x的回归方程;
(ⅱ)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸x为何值时,收益
,则当优等品的尺寸x为何值时,收益![]() 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)
附:对于样本![]()
![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,五边形![]() 中,四边形
中,四边形![]() 为长方形,
为长方形,![]() 为边长为
为边长为![]() 的正三角形,将
的正三角形,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.

(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值的绝对值.
所成二面角的余弦值的绝对值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 与
与![]() 轴、
轴、![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() ,
,![]() 两点.
两点.
(1)求线段![]() 中点
中点![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)若![]() 是(1)中点
是(1)中点![]() 的轨迹上的动点,求
的轨迹上的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com