练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，某海面上有、、三个小岛（面积大小忽略不计），岛在岛的北偏东方向距岛千米处，岛在岛的正东方向距岛20千米处.以为坐标原点，的正东方向为轴的正方向，1千米为单位长度，建立平面直角坐标系.圆经过、、三点.

    （1）求圆的方程；

    （2）若圆区域内有未知暗礁，现有一船D在岛的南偏西30°方向距岛40千米处，正沿着北偏东行驶，若不改变方向，试问该船有没有触礁的危险？

    【答案】（1）（2）该船有触礁的危险

    【解析】

    （1）由圆过点、、，设圆的方程为，

    再将点、、的坐标代入运算即可得解；

    （2）由题意可得该船航行方向为直线：，再结合点到直线的距离公式可得圆心到直线的距离，得解.

    解：（1）如图所示，、，

    设过、、三点的圆的方程为，

    得：，

    解得，，，

    故所以圆的方程为，

    圆心为，半径，

    （2）该船初始位置为点，则，

    且该船航线所在直线的斜率为1，

    故该船航行方向为直线：，

    由于圆心到直线的距离，

    故该船有触礁的危险.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若，求证：

    （2）若，恒有，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，动点到定点的距离与到定直线的距离的比为，动点的轨迹记为.

    （1）求轨迹的方程；

    （2）若点在轨迹上运动，点在圆上运动，且总有，

    求的取值范围；

    （3）过点的动直线交轨迹于两点，试问:在此坐标平面上是否存在一个定点，使得无论如何转动，以为直径的圆恒过点?若存在，求出点的坐标.若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大型商场去年国庆期间累计生成万张购物单，从中随机抽出张，对每单消费金额进行统计得到下表：

    消费金额（单位：元）

    购物单张数

    25

    25

    30

    10

    10

    由于工作人员失误，后两栏数据已无法辨识，但当时记录表明，根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率，完成下列问题：

    （1）估计去年国庆期间该商场累计生成的购物单中，单笔消费额超过元的概率；

    （2）为鼓励顾客消费，该商场打算在今年国庆期间进行促销活动，凡单笔消费超过元者，可抽奖一次，中一等奖、二等奖、三等奖的顾客可以分别获得价值元、元、元的奖品.已知中奖率为，且一等奖、二等奖、三等奖的中奖率依次构成等比数列，其中一等奖的中奖率为.若今年国庆期间该商场的购物单数量比去年同期增长，式预测商场今年国庆期间采办奖品的开销.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以原点为极点，轴的非负半轴为极轴建立极坐标系.已知曲线的极坐标方程为，为曲线上的动点，与轴、轴的正半轴分别交于，两点.

    （1）求线段中点的轨迹的参数方程；

    （2）若是（1）中点的轨迹上的动点，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于圆周率，数学发展史上出现过多很有创意的求法，如著名的蒲丰试验，受其启发，我们也可以通过设计下面的试验来估计的值，试验步骤如下：①先请高二年级名同学每人在小卡片上随机写下一个实数对；②若卡片上的，能与构成锐角三角形，则将此卡片上交；③统计上交的卡片数，记为；④根据统计数，估计的值.那么可以估计的值约为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公交公司为了方便市民出行，科学规划车辆投放，在一个人员密集流动地段增设一个起点站，为了研究车辆发车间隔时间x与乘客等候人数y之间的关系，经过调查得到如下数据：

    间隔时间x/分

    10

    11

    12

    13

    14

    15

    等候人数y/人

    23

    25

    26

    29

    28

    31

    调查小组先从这6组数据中选取4组数据求线性回归方程，再用剩下的2组数据进行检验.检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数，再求与实际等候人数y的差，若差值的绝对值都不超过1，则称所求方程是“恰当回归方程”.

    （1）从这6组数据中随机选取4组数据，求剩下的2组数据的间隔时间相邻的概率；

    （2）若选取的是中间4组数据，求y关于x的线性回归方程，并判断此方程是否是“恰当回归方程”.

    附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为：，.

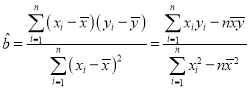    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆： 的离心率为，短轴端点与两焦点围成的三角形面积为.

    (1)求椭圆的方程；

    (2)设直线与椭圆交于两点，且过点，为坐标原点，当△为直角三角形，求直线的斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动点满足，记M的轨迹为曲线C，直线l：（）交曲线C于P，Q两点，点P在第一象限，轴，垂足为E，连接QE并延长交曲线C于点G.

    （1）求曲线C的方程，并说明曲线C是什么曲线；

    （2）若，求的面积.

    （3）求面积的最大值.

    查看答案和解析>>

    同步练习册答案