
【题目】椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,短轴端点与两焦点围成的三角形面积为
,短轴端点与两焦点围成的三角形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且过点
两点,且过点![]() ,
,![]() 为坐标原点,当△
为坐标原点,当△![]() 为直角三角形,求直线
为直角三角形,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() .
.
【解析】
(1)利用题中所给面积及离心率列出方程组求解a,b,c,即可求得椭圆的标准方程;(2)根据题意设出直线方程并与椭圆方程联立,得到关于x的二次方程,由韦达定理表示出![]() ,①当
,①当![]() 为直角时,由
为直角时,由![]() 列出方程即可求得k;②当
列出方程即可求得k;②当![]() 或
或![]() 为直角时,不妨设
为直角时,不妨设![]() 为直角,由
为直角,由![]() 及
及![]() 列出方程组求点A的坐标,从而求出直线的斜率k.
列出方程组求点A的坐标,从而求出直线的斜率k.
(1)根据题意可得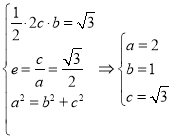 ,
,
所以椭圆方程为![]() ;
;
(2)根据题意,过点![]() 满足题意得直线斜率存在,设
满足题意得直线斜率存在,设![]() ,
,
联立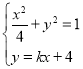 ,消去y得:
,消去y得:![]() ,
,
![]() ,令
,令![]() ,解得
,解得![]() ,
,
![]() ,
,
设A、B两点的坐标分别为![]() ,
,
①当![]() 为直角时,
为直角时,![]() ,即
,即![]() ,
,
所以![]() ,
,
则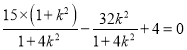 ,解得
,解得![]() ;
;
②当![]() 或
或![]() 为直角时,不妨设
为直角时,不妨设![]() 为直角,
为直角,
此时,![]() ,则
,则![]() ,
,![]() ①,
①,
又![]() ②,将①代入②可得
②,将①代入②可得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
将![]() 代入①,得
代入①,得![]() ,所以
,所以![]() ,
,
经检验,所求k值均与题意相符,综上,k的值为![]() 和
和![]() .
.


科目:高中数学 来源: 题型:
【题目】为了进一步推动全市学习型党组织、学习型社会建设,某市组织开展“学习强国”知识测试,每人测试文化、经济两个项目,每个项目满分均为60分.从全体测试人员中随机抽取了100人,分别统计他们文化、经济两个项目的测试成绩,得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下:

经济项目测试成绩频率分布直方图
分数区间 | 频数 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化项目测试成绩频数分布表
将测试人员的成绩划分为三个等级如下:分数在区间![]() 内为一般,分数在区间
内为一般,分数在区间![]() 内为良好,分数在区间
内为良好,分数在区间![]() 内为优秀.
内为优秀.
(1)在抽取的100人中,经济项目等级为优秀的测试人员中女生有14人,经济项目等级为一般或良好的测试人员中女生有34人.填写下面列联表,并根据列联表判断是否有![]() 以上的把握认为“经济项目等级为优秀”与性别有关?
以上的把握认为“经济项目等级为优秀”与性别有关?
优秀 | 一般或良好 | 合计 | |
男生数 | |||
女生数 | |||
合计 |
(2)用这100人的样本估计总体.
(i)求该市文化项目测试成绩中位数的估计值.
(ii)对该市文化项目、经济项目的学习成绩进行评价.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某海面上有![]() 、
、![]() 、
、![]() 三个小岛(面积大小忽略不计),
三个小岛(面积大小忽略不计),![]() 岛在
岛在![]() 岛的北偏东
岛的北偏东![]() 方向距
方向距![]() 岛
岛![]() 千米处,
千米处,![]() 岛在
岛在![]() 岛的正东方向距
岛的正东方向距![]() 岛20千米处.以
岛20千米处.以![]() 为坐标原点,
为坐标原点,![]() 的正东方向为
的正东方向为![]() 轴的正方向,1千米为单位长度,建立平面直角坐标系.圆
轴的正方向,1千米为单位长度,建立平面直角坐标系.圆![]() 经过
经过![]() 、
、![]() 、
、![]() 三点.
三点.

(1)求圆![]() 的方程;
的方程;
(2)若圆![]() 区域内有未知暗礁,现有一船D在
区域内有未知暗礁,现有一船D在![]() 岛的南偏西30°方向距
岛的南偏西30°方向距![]() 岛40千米处,正沿着北偏东
岛40千米处,正沿着北偏东![]() 行驶,若不改变方向,试问该船有没有触礁的危险?
行驶,若不改变方向,试问该船有没有触礁的危险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() 和
和![]() ,记过点
,记过点![]() ,
,![]() 的直线的斜率为k,问:是否存在m,使得
的直线的斜率为k,问:是否存在m,使得![]() ?若存在,求出m的值;若不存在,请说明理由.
?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌服装店为了庆祝开业两周年,特举办“你敢买,我就送”的回馈活动,规定店庆当日进店购买指定服装的消费者可参加游戏,赢取奖金,游戏分为以下两种:
游戏 1:参加该游戏赢取奖金的成功率为![]() ,成功后可获得
,成功后可获得![]() 元奖金;
元奖金;
游戏 2:参加该游戏赢取奖金的成功率为![]() ,成功后可得
,成功后可得![]() 元奖金;
元奖金;
无论参与哪种游戏,未成功均没有收获,每人有且仅有一次机会,且每次游戏成功与否均互不影响,游戏结束后可到收银台领取奖金。
(Ⅰ)已知甲参加游戏 1,乙参加游戏 2,记甲与乙获得的总奖金为![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若甲、乙、丙三人都选择游戏 1或都选择游戏 2,问:他们选择何种规则,累计得到奖金的数学期望值最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
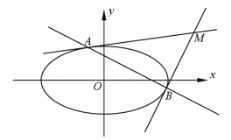
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(1)求![]() 的值;
的值;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为椭圆
为椭圆![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,设
,设![]() 的角平分线
的角平分线![]() 交椭圆
交椭圆![]() 的长轴于点
的长轴于点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面上定点![]() 到定直线
到定直线![]() 的距离
的距离![]() ,
,![]() 为该平面上的动点,过
为该平面上的动点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且
,且![]() ;
;

(1)试建立适当的平面直角坐标系,求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 、
、![]() 两点,交直线
两点,交直线![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com