
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离与
的距离与![]() 到定直线
到定直线![]() 的距离的比为
的距离的比为![]() ,动点
,动点![]() 的轨迹记为
的轨迹记为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若点![]() 在轨迹
在轨迹![]() 上运动,点
上运动,点![]() 在圆
在圆![]() 上运动,且总有
上运动,且总有![]() ,
,
求![]() 的取值范围;
的取值范围;
(3)过点![]() 的动直线
的动直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,试问:在此坐标平面上是否存在一个定点
两点,试问:在此坐标平面上是否存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
【答案】(1)![]() (2)
(2)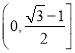
![]() (3)存在,
(3)存在,![]() 理由见解析
理由见解析
【解析】
(1)设点![]() ,由
,由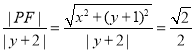 化简求解;(2)圆心
化简求解;(2)圆心![]() .根据圆与椭圆的位置关系,分两种情况讨论:①当
.根据圆与椭圆的位置关系,分两种情况讨论:①当![]() 时,②当
时,②当![]() 时,设
时,设![]() ,分别利用三角代换求得其最值,即可得到取值范围;(3)把
,分别利用三角代换求得其最值,即可得到取值范围;(3)把![]() 代入椭圆的方程可得:
代入椭圆的方程可得:![]() ,取点
,取点![]() 时满足
时满足![]() .然后证明:在此坐标平面上存在一个定点
.然后证明:在此坐标平面上存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() 即可.
即可.
(1)设点![]() ,由题意可得:
,由题意可得: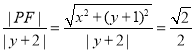 ,
,
即:![]() .
.
(2)圆心![]()
:①当![]() 时,∵总有
时,∵总有![]() ,
,![]()
∴![]()
.②当![]() 时,设
时,设![]() ,总有
,总有![]()
![]() ,
,
所以 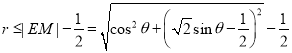
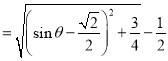 ,
,
∴![]() .
.
综上可得:![]() 的取值范围是
的取值范围是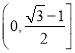 ∪
∪![]() .
.
(3)把![]() 代入椭圆的方程可得:
代入椭圆的方程可得:![]() ,
,
解得![]() .,所以
.,所以![]() ,
,![]() ,取点
,取点![]() 时满足
时满足![]() .
.
下面证明:存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.
设过点![]() 的动直线
的动直线![]() 的方程为:
的方程为:![]() ,
,![]() .
.
联立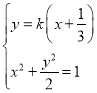 ,化为:
,化为:![]() ,
,
∴![]() ,
,![]() .
.
则![]()
![]()
![]()
![]()
∴在此坐标平面上存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.


科目:高中数学 来源: 题型:
【题目】为了进一步推动全市学习型党组织、学习型社会建设,某市组织开展“学习强国”知识测试,每人测试文化、经济两个项目,每个项目满分均为60分.从全体测试人员中随机抽取了100人,分别统计他们文化、经济两个项目的测试成绩,得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下:

经济项目测试成绩频率分布直方图
分数区间 | 频数 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化项目测试成绩频数分布表
将测试人员的成绩划分为三个等级如下:分数在区间![]() 内为一般,分数在区间
内为一般,分数在区间![]() 内为良好,分数在区间
内为良好,分数在区间![]() 内为优秀.
内为优秀.
(1)在抽取的100人中,经济项目等级为优秀的测试人员中女生有14人,经济项目等级为一般或良好的测试人员中女生有34人.填写下面列联表,并根据列联表判断是否有![]() 以上的把握认为“经济项目等级为优秀”与性别有关?
以上的把握认为“经济项目等级为优秀”与性别有关?
优秀 | 一般或良好 | 合计 | |
男生数 | |||
女生数 | |||
合计 |
(2)用这100人的样本估计总体.
(i)求该市文化项目测试成绩中位数的估计值.
(ii)对该市文化项目、经济项目的学习成绩进行评价.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为侧棱
为侧棱![]() 上一点.
上一点.
(Ⅰ)若![]() ,求证:
,求证:![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
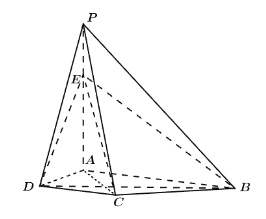
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于项数为![]() (
(![]() )的有穷正整数数列
)的有穷正整数数列![]() ,记
,记![]() (
(![]() ),即
),即![]() 为
为![]() 中的最大值,称数列
中的最大值,称数列![]() 为数列
为数列![]() 的“创新数列”.比如
的“创新数列”.比如![]() 的“创新数列”为
的“创新数列”为![]() .
.
(1)若数列![]() 的“创新数列”
的“创新数列”![]() 为1,2,3,4,4,写出所有可能的数列
为1,2,3,4,4,写出所有可能的数列![]() ;
;
(2)设数列![]() 为数列
为数列![]() 的“创新数列”,满足
的“创新数列”,满足![]() (
(![]() ),求证:
),求证: ![]() (
(![]() );
);
(3)设数列![]() 为数列
为数列![]() 的“创新数列”,数列
的“创新数列”,数列![]() 中的项互不相等且所有项的和等于所有项的积,求出所有的数列
中的项互不相等且所有项的和等于所有项的积,求出所有的数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为直角坐标原点,以极轴为
为直角坐标原点,以极轴为![]() 轴的正半轴建立平面直角坐标系
轴的正半轴建立平面直角坐标系![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的
个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的![]() ,纵坐标保持不变,得到曲线
,纵坐标保持不变,得到曲线![]()
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某海面上有![]() 、
、![]() 、
、![]() 三个小岛(面积大小忽略不计),
三个小岛(面积大小忽略不计),![]() 岛在
岛在![]() 岛的北偏东
岛的北偏东![]() 方向距
方向距![]() 岛
岛![]() 千米处,
千米处,![]() 岛在
岛在![]() 岛的正东方向距
岛的正东方向距![]() 岛20千米处.以
岛20千米处.以![]() 为坐标原点,
为坐标原点,![]() 的正东方向为
的正东方向为![]() 轴的正方向,1千米为单位长度,建立平面直角坐标系.圆
轴的正方向,1千米为单位长度,建立平面直角坐标系.圆![]() 经过
经过![]() 、
、![]() 、
、![]() 三点.
三点.

(1)求圆![]() 的方程;
的方程;
(2)若圆![]() 区域内有未知暗礁,现有一船D在
区域内有未知暗礁,现有一船D在![]() 岛的南偏西30°方向距
岛的南偏西30°方向距![]() 岛40千米处,正沿着北偏东
岛40千米处,正沿着北偏东![]() 行驶,若不改变方向,试问该船有没有触礁的危险?
行驶,若不改变方向,试问该船有没有触礁的危险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
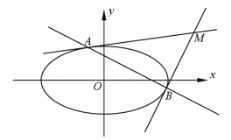
(1)求![]() 的值;
的值;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com