【题目】已知定点，动点在轴上运动，过点作直线交轴于点，延长至点，使．点的轨迹是曲线．

（1）求曲线的方程；

（2）若，是曲线上的两个动点，满足，证明：直线过定点；

（3）若直线与曲线交于，两点，且，，求直线的斜率的取值范围．

【题目】在平面直角坐标系中，对于点，若函数满足：，都有，就称这个函数是点的“限定函数”．以下函数：①，②，③，④，其中是原点的“限定函数”的序号是______．已知点在函数的图象上，若函数是点的“限定函数”，则的取值范围是______．

【题目】设和是双曲线上的两点，线段的中点为，直线不经过坐标原点．

（1）若直线和直线的斜率都存在且分别为和，求证：；

（2）若双曲线的焦点分别为、，点的坐标为，直线的斜率为，求由四点、、、所围成四边形的面积．

【题目】教材曾有介绍：圆上的点处的切线方程为。我们将其结论推广：椭圆上的点处的切线方程为，在解本题时可以直接应用。已知，直线与椭圆有且只有一个公共点.

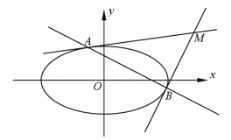
（1）求的值；

（2）设为坐标原点，过椭圆上的两点、分别作该椭圆的两条切线、，且与交于点。当变化时，求面积的最大值；

（3）在（2）的条件下，经过点作直线与该椭圆交于、两点，在线段上存在点，使成立，试问：点是否在直线上，请说明理由.

【题目】已知椭圆 ： （ ）的离心率 ，直线 被以椭圆 的短轴为直径的圆截得的弦长为 .

（1）求椭圆 的方程；

（2）过点 的直线 交椭圆于 ， 两个不同的点，且 ，求 的取值范围.

【题目】已知数列{an}满足：，且an+1（n=1，2…）集合M={an|}中的最小元素记为m.

（1）若a1=20，写出m和a10的值：

（2）若m为偶数，证明：集合M的所有元素都是偶数；

（3）证明：当且仅当时，集合M是有限集.

（1）当点B是W的顶点，且四边形ABCD为正方形时，求此正方形的面积；

（2）当点B不是W的顶点时，判断四边形ABCD是否可能为正方形，并说明理由.

（1）求曲线y=f（x）在点（1，f（1））处的切线方程：

（2）若非零实数a使得f（x）axax2对x∈[1，+∞）恒成立，求a的取值范围.

【题目】如图，四棱锥的底面是菱形，底面，分别是的中点，，，.

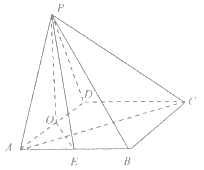
（I）证明：；

（II）求直线与平面所成角的正弦值；

（III）在边上是否存在点，使与所成角的余弦值为，若存在，确定点位置；若不存在，说明理由.

（1）求证：MN//平面DCC1D1；

（2）求证：MN⊥平面ADC1；

（3）求三棱锥D1﹣ADC1的体积.