
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出当![]() 时直线
时直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 为直线
为直线![]() 上的动点,
上的动点,![]() ,过
,过![]() 作直线
作直线![]() 的垂线
的垂线![]() ,
,![]() 交
交![]() 的中垂线于点
的中垂线于点![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() ,
, ![]() ,
,![]() ,
,![]() , PA=AB=BC=2. E是PC的中点.
, PA=AB=BC=2. E是PC的中点.

(1)证明: ![]() ;
;
(2)求三棱锥P-ABC的体积;
(3) 证明:![]() 平面
平面![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】
某中学高二年级共有8个班,现从高二年级选10名同学组成社区服务小组,其中高二(1)班选取3名同学,其它各班各选取1名同学.现从这10名同学中随机选取3名同学到社区老年中心参加“尊老爱老”活动(每位同学被选到的可能性相同).
(1)求选出的3名同学来自不同班级的概率;
(2)设![]() 为选出的同学来自高二(1)班的人数,求随机变量
为选出的同学来自高二(1)班的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.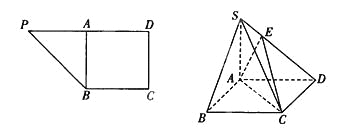
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥PABCD中,底面ABCD是菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
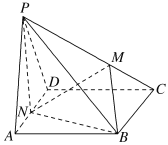
(1)求证:AD⊥平面PNB;
(2)若平面PAD⊥平面ABCD,求三棱锥PNBM的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下面四个命题:
①“直线![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() 平面
平面![]() ”;
”;
②“直线![]() 直线
直线![]() ”的充要条件是“
”的充要条件是“![]() 平行于
平行于![]() 所在的平面”;
所在的平面”;
③“直线![]() ,
,![]() 为异面直线”的充分不必要条件是“直线
为异面直线”的充分不必要条件是“直线![]() ,
,![]() 不相交”;
不相交”;
④“平面![]() 平面
平面![]() ”的必要不充分条件是“
”的必要不充分条件是“![]() 内存在不共线三点到
内存在不共线三点到![]() 的距离相等”.
的距离相等”.
其中正确命题的序号是____________________
查看答案和解析>>
科目: 来源: 题型:
【题目】槟榔原产于马来西亚,中国主要分布在云南、海南及台湾等热带地区,亚洲热带地区广泛栽培.槟榔是重要的中药材,南方一些少数民族还有将果实作为一种咀嚼嗜好品,但其被世界卫生组织国际癌症研究机构列为致癌物清单Ⅰ类致癌物.云南某民族中学为了解![]() ,
,![]() 两个少数民族班的学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名学生进行调查,经他们平均每周咀嚼槟榔的颗数作为样本,绘制成如图所示的茎叶图(图中的茎表示十位数字,叶表示个位数字).
两个少数民族班的学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名学生进行调查,经他们平均每周咀嚼槟榔的颗数作为样本,绘制成如图所示的茎叶图(图中的茎表示十位数字,叶表示个位数字).

(1)你能否估计哪个班的学生平均每周咀嚼槟榔的颗数较多?
(2)在被抽取的10名学生中,从平均每周咀嚼槟榔的颗数不低于20颗的学生中随机抽取3名学生,求抽到![]() 班学生人数
班学生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com