
科目: 来源: 题型:
【题目】下表是我省某地区2012年至2018年农村居民家庭年纯收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年纯收入 | 2 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2018年该地区农村居民家庭年纯收入的变化情况,并预测该地区2019年农村居民家庭年纯收入(结果精确到0.1)。
附:回归直线的斜率和截距的最小二乘法估计公式分别为: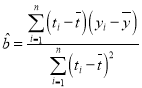 ,
,![]() 。
。
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次田径比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示。

若将运动员按成绩由好到差编为1—35号,再用系统抽样方法从中抽取5人,则其中成绩在区间![]() 上的运动员人数为
上的运动员人数为
A.6B.5C.4D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】某媒体对“男女延迟退休″这一公众关注的问题进行名意调查,如表是在某单位得到的数据:
赞同 | 反对 | 合计 | |
男 | 50 | 150 | 200 |
女 | 30 | 170 | 200 |
合计 | 80 | 320 | 400 |
(I)能否有97.5%的把握认为对这一问题的看法与性别有关?
(II)从赞同“男女延迟退休”的80人中,利用分层抽样的方法抽出8人,然后从中选出3人进行陈述发言,设发言的女士人数为X,求X的分布列和期望.
参考公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,该椭圆的离心率为
,该椭圆的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(I)求椭圆![]() 的方程;
的方程;
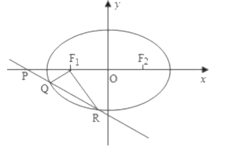
(Ⅱ)如图,若斜率为![]() 的直线
的直线![]() 与
与![]() 轴,椭圆
轴,椭圆![]() 顺次交于
顺次交于![]() 点在椭圆左顶点的左侧)且
点在椭圆左顶点的左侧)且![]() ,求证:直线
,求证:直线![]() 过定点;并求出斜率
过定点;并求出斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大型商场为迎接新年的到来,在自动扶梯![]() 的C点的上方悬挂竖直高度为5米的广告牌DE.如图所示,广告牌底部点E正好为DC的中点,电梯AC的坡度
的C点的上方悬挂竖直高度为5米的广告牌DE.如图所示,广告牌底部点E正好为DC的中点,电梯AC的坡度![]() .某人在扶梯上点P处(异于点C)观察广告牌的视角
.某人在扶梯上点P处(异于点C)观察广告牌的视角![]() .当人在A点时,观测到视角∠DAE的正切值为
.当人在A点时,观测到视角∠DAE的正切值为![]() .
.
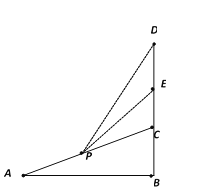
(1)求扶梯AC的长
(2)当某人在扶梯上观察广告牌的视角θ最大时,求CP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为积极响应国家“阳光体育运动”的号召,某学校在了解到学生的实际运动情况后,发起以“走出教室,走到操场,走到阳光”为口号的课外活动倡议,为调查该校学生每周平均体育运动时间的情况,从高一高二(非毕业年级)与高三(毕业年级)共三个年级学生中按照![]() 的比例分层抽样,收集
的比例分层抽样,收集![]() 位学生每周平均体育运动时间的样本数据(单位:小时),得到如图所示的频率分布直方图.(已知高一年级共有
位学生每周平均体育运动时间的样本数据(单位:小时),得到如图所示的频率分布直方图.(已知高一年级共有![]() 名学生)
名学生)
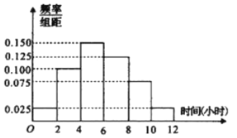
(1)据图估计该校学生每周平均体育运动时间,并估计高一年级每周平均体育运动时间不足![]() 小时的人数;
小时的人数;
(2)规定每周平均体育运动时间不少于![]() 小时记为“优秀”,否则为“非优秀”,在样本数据中,有
小时记为“优秀”,否则为“非优秀”,在样本数据中,有![]() 位高三学生的每周平均体育运动时间不少于
位高三学生的每周平均体育运动时间不少于![]() 小时,请完成下列
小时,请完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间是否优秀与毕业年级有关”?
的把握认为“该校学生的每周平均体育运动时间是否优秀与毕业年级有关”?
非毕业年级 | 毕业年级 | 合计 | |
优秀 | |||
非优秀 | |||
合计 |
|
附: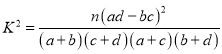 .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com