
科目: 来源: 题型:
【题目】随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,SF快递收取快递费的标准是:重量不超过1kg的包裹收费10元;重量超过1kg的包裹,在收费10元的基础上,每超过1kg(不足1kg,按1kg计算)需再收5元.某县SF分代办点将最近承揽的100件包裹的重量统计如下:
重量(单位:kg) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
件数 | 43 | 30 | 15 | 8 | 4 |
对近60天,每天揽件数量统计如下表:
件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
件数 | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 1 | 6 |
以上数据已做近似处理,将频率视为概率.
(1)计算该代办未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年开始,国家逐步推行全新的高考制度,新高考不再分文理科。某省采用![]() 模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某学校从高一年级1000名学生(其中男生550人,女生450人)中,根据性别分层,采用分层抽样的方法从中抽取100名学生进行调查.
模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某学校从高一年级1000名学生(其中男生550人,女生450人)中,根据性别分层,采用分层抽样的方法从中抽取100名学生进行调查.
(1)学校计划在高一上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的100名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),如下表是根据调查结果得到的![]() 列联表.请求出
列联表.请求出![]() 和
和![]() ,并判断是否有
,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“历史” | 总计 | |
男生 |
| 10 | |
女生 | 25 |
| |
总计 |
(2)在抽取到的女生中按(1)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中随机抽取4人,设这4人中选择“历史”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: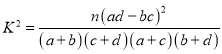
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A. 在统计学中,回归分析是检验两个分类变量是否有关系的一种统计方法
B. 线性回归方程对应的直线![]() 至少经过其样本数据点中的
至少经过其样本数据点中的![]() ,
,![]() ,
,![]()
![]() 一个点
一个点
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 在回归分析中,相关指数![]() 为
为![]() 的模型比相关指数
的模型比相关指数![]() 为
为![]() 的模型拟合的效果差
的模型拟合的效果差
查看答案和解析>>
科目: 来源: 题型:
【题目】记抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线上,
在抛物线上,![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,直线
,直线![]() 的斜率都存在,且
的斜率都存在,且![]() ;探究:直线
;探究:直线![]() 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“沉鱼、落雁、闭月、羞花”是由精彩故事组成的历史典故.“沉鱼”,讲的是西施浣纱的故事;“落雁”,指的就是昭君出塞的故事;“闭月”,是述说貂蝉拜月的故事;“羞花”,谈的是杨贵妃醉酒观花时的故事.她们分别是中国古代的四大美女.某艺术团要以四大美女为主题排演一部舞蹈剧,已知乙扮演杨贵妃,甲、丙、丁三人抽签决定扮演的对象,则甲不扮演貂蝉且丙扮演昭君的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com