
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若直线![]() 为曲线
为曲线![]() 的切线,求证:直线
的切线,求证:直线![]() 与曲线
与曲线![]() 不可能有2个切点.
不可能有2个切点.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)首先确定函数定义域和导函数;令![]() ,得到
,得到![]() ;当
;当![]() 时,
时,![]() ,得到函数单调递增;当
,得到函数单调递增;当![]() 时,分为两根都小于零和都大于零两种情况,根据导函数的符号得到原函数的单调区间;(2)采用反证法,假设可能有
时,分为两根都小于零和都大于零两种情况,根据导函数的符号得到原函数的单调区间;(2)采用反证法,假设可能有![]() 个切点;分别列出在两个切点的切线方程,根据方程相同可建立方程组,整理可得
个切点;分别列出在两个切点的切线方程,根据方程相同可建立方程组,整理可得![]() ;令
;令![]() ,构造函数
,构造函数![]() ,可利用导数求得
,可利用导数求得![]() ,等式不成立,从而得到假设错误,证得结论.
,等式不成立,从而得到假设错误,证得结论.
(1)由题意得:![]() 定义域为
定义域为![]() ,
,![]()
令![]() ,则
,则![]()
若![]() ,则
,则![]() ,则
,则![]() ,
,
![]() 函数
函数![]() 在
在![]() 上单调递增;
上单调递增;
若![]() 或
或![]() ,
,![]() 有两个零点
有两个零点![]() ,
,![]() ,则
,则![]()
其中![]() ,
,![]() ;
;
若![]() ,则
,则![]() ,
,![]() ,此时
,此时![]()
故函数![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,则
,则![]() ,
,![]()
此时当![]() 和
和![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 函数
函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
综上所述:当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为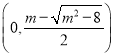 ,
,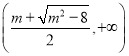 ;单调递减区间为
;单调递减区间为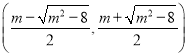
(2)假设存在一条直线与函数![]() 的图象有两个不同切点
的图象有两个不同切点![]() ,
,![]()
不妨令![]()
则![]() 处切线
处切线![]() 的方程为:
的方程为:![]()
![]() 处切线
处切线![]() 的方程为:
的方程为:![]()
![]() 为同一直线
为同一直线 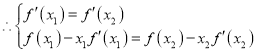
即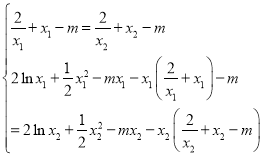 ,整理得:
,整理得: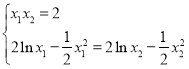
消去![]() 得:
得:![]() …①
…①
令![]() ,由
,由![]() 与
与![]() 得:
得:![]()
记![]() ,则
,则![]()
![]() 为
为![]() 上的单调减函数
上的单调减函数 ![]()
从而①式不可能成立,即假设不成立
![]() 若直线
若直线![]() 为曲线
为曲线![]() 的切线,则直线
的切线,则直线![]() 与曲线
与曲线![]() 不可能有
不可能有![]() 个切点
个切点


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且与直线
,且与直线![]() 相切.
相切.

(1)求椭圆的标准方程;
(2)过椭圆上点![]() 作椭圆的弦
作椭圆的弦![]() ,
,![]() ,若
,若![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,若
,若![]() 平行于
平行于![]() ,则
,则![]() ,
,![]() 斜率之和是否为定值?
斜率之和是否为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,SF快递收取快递费的标准是:重量不超过1kg的包裹收费10元;重量超过1kg的包裹,在收费10元的基础上,每超过1kg(不足1kg,按1kg计算)需再收5元.某县SF分代办点将最近承揽的100件包裹的重量统计如下:
重量(单位:kg) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
件数 | 43 | 30 | 15 | 8 | 4 |
对近60天,每天揽件数量统计如下表:
件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
件数 | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 1 | 6 |
以上数据已做近似处理,将频率视为概率.
(1)计算该代办未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市采购了一批袋装的进口牛肉干进行销售,共1000袋,每袋成本为30元,销售价格为50元,经过科学测定,每袋牛肉干变质的概率为![]() ,且各袋牛肉干是否变质相互独立.依据消费者权益保护法的规定:超市出售变质食品的,消费者可以要求超市退一赔三.为了保护消费者权益,针对购买到变质牛肉干的消费者,超市除退货外,并对每袋牛肉干以销售价格的三倍现金赔付,且把变质牛肉干做废物处理,不再进行销售.
,且各袋牛肉干是否变质相互独立.依据消费者权益保护法的规定:超市出售变质食品的,消费者可以要求超市退一赔三.为了保护消费者权益,针对购买到变质牛肉干的消费者,超市除退货外,并对每袋牛肉干以销售价格的三倍现金赔付,且把变质牛肉干做废物处理,不再进行销售.
(1)若销售完这批牛肉干后得到的利润为X,且![]() ,求p的取值范围;
,求p的取值范围;
(2)已知![]() ,若超市聘请兼职员工来检查这批牛肉干是否变质,超市需要支付兼职员工工资5000元,这样检查到的变质牛肉干直接当废物处理,就不会流入到消费者手中.请以超市获取的利润为决策依据,判断超市是否需要聘请兼职员工来检验这批牛肉干是否变质?
,若超市聘请兼职员工来检查这批牛肉干是否变质,超市需要支付兼职员工工资5000元,这样检查到的变质牛肉干直接当废物处理,就不会流入到消费者手中.请以超市获取的利润为决策依据,判断超市是否需要聘请兼职员工来检验这批牛肉干是否变质?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 是
是![]() 的导函数,则下列结论中错误的个数是( )
的导函数,则下列结论中错误的个数是( )
①函数![]() 的值域与
的值域与![]() 的值域相同;
的值域相同;
②若![]() 是函数
是函数![]() 的极值点,则
的极值点,则![]() 是函数
是函数![]() 的零点;
的零点;
③把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,就可以得到
个单位长度,就可以得到![]() 的图像;
的图像;
④函数![]() 和
和![]() 在区间
在区间![]() 内都是增函数.
内都是增函数.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com