
科目: 来源: 题型:
【题目】近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000t生活垃圾.经分拣以后数据统计如下表(单位:![]() ):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
厨余垃圾”箱 | 可回收物”箱 | 其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
A.厨余垃圾投放正确的概率为![]()
B.居民生活垃圾投放错误的概率为![]()
C.该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱
D.厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 分别作射线
分别作射线![]() 、
、![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,且以
,且以![]() 为直径的圆经过点
为直径的圆经过点![]() .试探究直线
.试探究直线![]() 是否过定点?如果是,请求出该定点;如果不是,请说明理由.
是否过定点?如果是,请求出该定点;如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
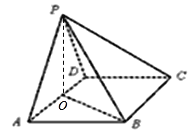
(Ⅰ)若PA=PD,求证:平面POB⊥平面PAD;
(Ⅱ)若平面PAD⊥平面ABCD,且PA=PD=AD=2,试问在线段PC上是否存在点M,使二面角M-BO-C的大小为30°,如存在,求![]() 的值,如不存在,说明理由.
的值,如不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
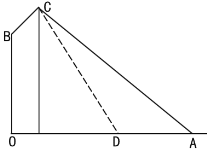
【题目】如图,在路边安装路灯:路宽![]() 米,灯杆长
米,灯杆长![]() 米,且与灯柱
米,且与灯柱![]() 成120°角,路灯采用锥形灯罩,灯罩轴线
成120°角,路灯采用锥形灯罩,灯罩轴线![]() 与灯杆垂直且正好通过道路路面的中线.
与灯杆垂直且正好通过道路路面的中线.
(1)求灯柱高![]() 的长度(精确到0.01米);
的长度(精确到0.01米);
(2)若该路灯投射出的光成一个圆锥体,该圆锥体母线与轴线的夹角是30°,写出路灯在路面上投射出的截面图形的边界是什么曲线?写出其相应的几何量(精确到0.01米).
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),将C上每一点的横坐标保持不变,纵坐标变为原来的3倍,得曲线C1.以O为极点,x轴正半轴为极轴建立极坐标系.
(α为参数),将C上每一点的横坐标保持不变,纵坐标变为原来的3倍,得曲线C1.以O为极点,x轴正半轴为极轴建立极坐标系.
(1)求C1的极坐标方程
(2)设M,N为C1上两点,若OM⊥ON,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,都有
,都有![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“
为“![]() 函数”。
函数”。
(1)试判断函数![]() 是否是“
是否是“![]() 函数”并说明理由;
函数”并说明理由;
(2)若函数![]() 为“
为“![]() 函数”,求实数
函数”,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 为“
为“![]() 函数”,且
函数”,且![]() .
.
求证(![]() )
)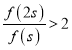 ;
;
(![]() )对任意
)对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com